
【題目】設定義在D上的函數![]() 在點
在點![]() 處的切線方程為
處的切線方程為![]() ,當
,當![]() 時,若
時,若![]() 在D內恒成立,則稱P點為函數
在D內恒成立,則稱P點為函數![]() 的“類對稱中心點”,則函數
的“類對稱中心點”,則函數![]() 的“類對稱中心點”的坐標是________.
的“類對稱中心點”的坐標是________.
【答案】![]()
【解析】
由求導公式求出函數f(x)的導數,由導數的幾何意義和條件求出切線方程,再求出y=g(x),設F(x)=f(x)﹣g(x),求出導數化簡后利用分類討論和導數與函數單調性的關系,判斷出F(x)的單調性和最值,從而可判斷出![]() 的符號,再由“類對稱中心點”的定義確定“類對稱中心點”的坐標.
的符號,再由“類對稱中心點”的定義確定“類對稱中心點”的坐標.
解:由題意得,f′(x)![]() ,f(x0)
,f(x0)![]() (x>0),
(x>0),
即函數y=f(x)的定義域D=(0,+∞),
所以函數y=f(x)在點P(x0,f(x0))處的切線方程l方程為:
y﹣(![]() )=(
)=(![]() )(x﹣x0),
)(x﹣x0),
則g(x)=(![]() )(x﹣x0)+(
)(x﹣x0)+(![]() ),
),
設F(x)=f(x)﹣g(x)![]() lnx﹣[(
lnx﹣[(![]() )(x﹣x0)+(
)(x﹣x0)+(![]() )],
)],
則F(x0)=0,
所以F′(x)=f′x)﹣g′(x)![]() (
(![]() )
)![]()
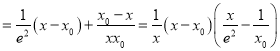
當0<x0<e時,F(x)在(x0,![]() )上遞減,
)上遞減,
∴x∈(x0,![]() )時,F(x)<F(x0)=0,此時
)時,F(x)<F(x0)=0,此時![]() ,
,
當x0>e時,F(x)在(![]() ,x0)上遞減;
,x0)上遞減;
∴x∈(![]() ,x0)時,F(x)>F(x0)=0,此時
,x0)時,F(x)>F(x0)=0,此時![]() ,
,
∴y=F(x)在(0,e)∪(e,+∞)上不存在“類對稱點”.
若x0=e,![]() 0,則F(x)在(0,+∞)上是增函數,
0,則F(x)在(0,+∞)上是增函數,
當x>x0時,F(x)>F(x0)=0,當x<x0時,F(x)<F(x0)=0,
故![]() ,
,
即此時點P是y=f(x)的“類對稱點”,
綜上可得,y=F(x)存在“類對稱點”,e是一個“類對稱點”的橫坐標,
又f(e)![]() ,所以函數f(x)的“類對稱中心點”的坐標是
,所以函數f(x)的“類對稱中心點”的坐標是![]() ,
,
故答案為:![]() .
.


 期末集結號系列答案
期末集結號系列答案科目:高中數學 來源: 題型:
【題目】至![]() 年底,我國發明專利申請量已經連續
年底,我國發明專利申請量已經連續![]() 年位居世界首位,下表是我國
年位居世界首位,下表是我國![]() 年至
年至![]() 年發明專利申請量以及相關數據.
年發明專利申請量以及相關數據.
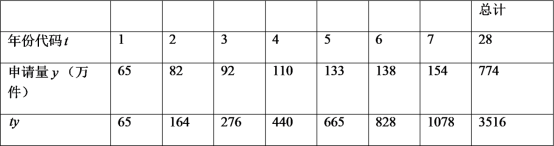
注:年份代碼![]() ~
~![]() 分別表示
分別表示![]() ~
~![]() .
.
(1)可以看出申請量每年都在增加,請問這幾年中哪一年的增長率達到最高,最高是多少?
(2)建立![]() 關于
關于![]() 的回歸直線方程(精確到
的回歸直線方程(精確到![]() ),并預測我國發明專利申請量突破
),并預測我國發明專利申請量突破![]() 萬件的年份.
萬件的年份.
參考公式:回歸直線的斜率和截距的最小二乘法估計分別為 ,
,![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在如圖所示的幾何體中,四邊形ABCD是正方形,PA⊥平面ABCD,E,F分別是線段AD,PB的中點,PA=AB=1.
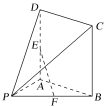
(1)證明:EF∥平面PDC;
(2)求點F到平面PDC的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數集![]() (
(![]() ,
,![]() )具有性質
)具有性質![]() :對任意的
:對任意的![]() 、
、![]() (
(![]() ),
),![]() 與
與![]() 兩數中至少有一個屬于
兩數中至少有一個屬于![]() .
.
(1)分別判斷數集![]() 與
與![]() 是否具有性質
是否具有性質![]() ,并說明理由;
,并說明理由;
(2)證明:![]() ,且
,且![]() ;
;
(3)證明:當![]() 時,
時,![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 成等比數列.
成等比數列.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知在四棱錐S﹣AFCD中,平面SCD⊥平面AFCD,∠DAF=∠ADC=90°,AD=1,AF=2DC=4,![]() ,B,E分別為AF,SA的中點.
,B,E分別為AF,SA的中點.
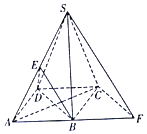
(1)求證:平面BDE∥平面SCF
(2)求二面角A﹣SC﹣B的余弦值
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com