
【題目】如圖,已知在四棱錐S﹣AFCD中,平面SCD⊥平面AFCD,∠DAF=∠ADC=90°,AD=1,AF=2DC=4,![]() ,B,E分別為AF,SA的中點.
,B,E分別為AF,SA的中點.
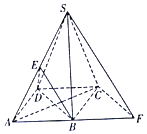
(1)求證:平面BDE∥平面SCF
(2)求二面角A﹣SC﹣B的余弦值
【答案】(1)證明見解析(2)![]()
【解析】
(1)通過證明![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,由此證得平面
,由此證得平面![]() 平面
平面![]() .
.
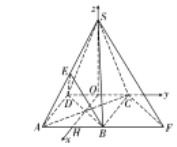
(2)取CD的中點O,連結(jié)SO,取AB的中點H,連結(jié)OH.證得![]() 兩兩垂直,由此建立空間直角坐標(biāo)系,通過平面
兩兩垂直,由此建立空間直角坐標(biāo)系,通過平面![]() 和平面
和平面![]() 的法向量,計算出二面角的余弦值.
的法向量,計算出二面角的余弦值.
(1)證明:∵∠DAF=∠ADC=90°,∴DC∥AF,
又B為AF的中點,∴四邊形BFCD是平行四邊形,∴CF∥BD,
∵BD平面BDE,CF平面BDE,
∴CF∥平面BDE,
∵B,E分別是AF,SA的中點,∴SF∥BE,
∵BE平面BDE,SF平面BDE,
∴SF∥平面BDE,
又CF∩SF=F,∴平面BDE∥平面SCF.
(2)取CD的中點O,連結(jié)SO,
∵△SCD是等腰三角形,O是CD中點,∴SO⊥CD,
又平面SCD⊥平面AFCD,平面SCD∩平面AFCD=CD,
∴SO⊥平面AFCD,取AB的中點H,連結(jié)OH,
由題設(shè)知四邊形ABCD是矩形,∴OH⊥CD,SO⊥OH,
以O為原點,OH為x軸,OC為y軸,OS為z軸,建立空間直角坐標(biāo)系,
則A(1,﹣1,0),B(1,1,0),C(0,1,0),S(0,0,1),
∴![]() (1,﹣2,0),
(1,﹣2,0),![]() (0,﹣1,1),
(0,﹣1,1),![]() (1,0,0),
(1,0,0),
設(shè)平面ASC的法向量![]() (x,y,z),
(x,y,z),
則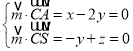 ,取y=
,取y=![]() (2,1,1),
(2,1,1),
設(shè)平面BSC的法向量![]() (x,y,z),
(x,y,z),
則 ,取y=1,得
,取y=1,得![]() (0,1,1),
(0,1,1),
∴cos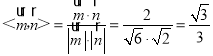 ,
,
由圖知二面角A﹣SC﹣B的平面角為銳角,
∴二面角A﹣SC﹣B的余弦值為![]() .
.


 新課標(biāo)同步訓(xùn)練系列答案
新課標(biāo)同步訓(xùn)練系列答案 一線名師口算應(yīng)用題天天練一本全系列答案
一線名師口算應(yīng)用題天天練一本全系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)定義在D上的函數(shù)![]() 在點
在點![]() 處的切線方程為
處的切線方程為![]() ,當(dāng)
,當(dāng)![]() 時,若
時,若![]() 在D內(nèi)恒成立,則稱P點為函數(shù)
在D內(nèi)恒成立,則稱P點為函數(shù)![]() 的“類對稱中心點”,則函數(shù)
的“類對稱中心點”,則函數(shù)![]() 的“類對稱中心點”的坐標(biāo)是________.
的“類對稱中心點”的坐標(biāo)是________.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)求函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)證明:對任意的![]() ,存在唯一的
,存在唯一的![]() ,使
,使![]() ;
;
(3)設(shè)(2)中所確定的![]() 關(guān)于
關(guān)于![]() 的函數(shù)為
的函數(shù)為![]() ,證明:當(dāng)
,證明:當(dāng)![]() 時,有
時,有![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】根據(jù)如圖給出的2005年至2016年我國人口總量及增長率的統(tǒng)計圖,以下結(jié)論不正確的是![]()
![]()
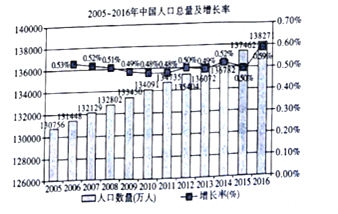
A. 自2005年以來,我國人口總量呈不斷增加趨勢
B. 自2005年以來,我國人口增長率維持在![]() 上下波動
上下波動
C. 從2005年后逐年比較,我國人口增長率在2016年增長幅度最大
D. 可以肯定,在2015年以后,我國人口增長率將逐年變大
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系xOy中,曲線C的參數(shù)方程為![]() (α為參數(shù)),在以坐標(biāo)原點O為極點,x軸的正半軸為極軸的極坐標(biāo)系中,點P的極坐標(biāo)為
(α為參數(shù)),在以坐標(biāo)原點O為極點,x軸的正半軸為極軸的極坐標(biāo)系中,點P的極坐標(biāo)為![]() ,直線l的極坐標(biāo)方程為
,直線l的極坐標(biāo)方程為![]() .
.
(1)求直線l的直角坐標(biāo)方程與曲線C的普通方程;
(2)若Q是曲線C上的動點,M為線段PQ的中點,直線l上有兩點A,B,始終滿足|AB|=4,求△MAB面積的最大值與最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在四棱錐![]() 中,已知棱
中,已知棱![]() ,
,![]() ,
,![]() 兩兩垂直,長度分別為1,2,2.若
兩兩垂直,長度分別為1,2,2.若![]() (
(![]() ),且向量
),且向量![]() 與
與![]() 夾角的余弦值為
夾角的余弦值為![]() .
.
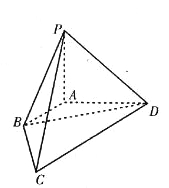
(1)求![]() 的值;
的值;
(2)求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,若點
,若點![]() 在
在![]() 的圖像上運動,則點
的圖像上運動,則點![]() 在
在![]() 的圖象上運動
的圖象上運動
(1)求![]() 的最小值,及相應(yīng)的
的最小值,及相應(yīng)的![]() 值
值
(2)求函數(shù)![]() 的解析式,指出其定義域
的解析式,指出其定義域![]() ,判斷并證明
,判斷并證明![]() 在
在![]() 上的單調(diào)性
上的單調(diào)性
(3)在函數(shù)![]() 和
和![]() 的圖象上是否分別存在點
的圖象上是否分別存在點![]() 關(guān)于直線
關(guān)于直線![]() 對稱,若存在,求出點
對稱,若存在,求出點![]() 的坐標(biāo);若不存在,請說明理由
的坐標(biāo);若不存在,請說明理由
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com