
| A. | ${(x+\sqrt{2})^2}+{(y+1)^2}=2$ | B. | ${(x+1)^2}+{(y+\sqrt{2})^2}=2$ | C. | ${(x-\sqrt{2})^2}+{(y-1)^2}=2$ | D. | ${(x-1)^2}+{(y-\sqrt{2})^2}=2$ |
科目:高中數學 來源: 題型:選擇題
| A. | (1,2) | B. | [1,2] | C. | (1,3) | D. | (1,$\frac{3}{2}$) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
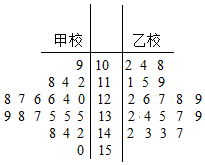 某市在對高三學生的4月理科數學調研測試的數據統計顯示,全市10000名學生的成績服從正態分布X~N(110,144),現從甲校100分以上的200份試卷中用系統抽樣的方法抽取了20份試卷來分析,統計如下:
某市在對高三學生的4月理科數學調研測試的數據統計顯示,全市10000名學生的成績服從正態分布X~N(110,144),現從甲校100分以上的200份試卷中用系統抽樣的方法抽取了20份試卷來分析,統計如下:| 試卷編號 | n1 | n2 | n3 | n4 | n5 | n6 | n7 | n8 | n9 | n10 |
| 試卷得分 | 109 | 118 | 112 | 114 | 126 | 128 | 127 | 124 | 126 | 120 |
| 試卷編號 | n11 | n12 | n13 | n14 | n15 | n16 | n17 | n18 | n19 | n20 |
| 試卷得分 | 135 | 138 | 135 | 137 | 135 | 139 | 142 | 144 | 148 | 150 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 若事件A與事件B互斥,則事件A與事件B對立 | |
| B. | 函數y=$\sqrt{{x}^{2}+9}+\frac{1}{\sqrt{{x}^{2}+9}}$(x∈R)的最小值為2 | |
| C. | 若直線(m+1)x+my-2=0與直線mx-2y+5=0互相垂直,則m=1 | |
| D. | “p∧q為真命題”是“p∨q為真命題”的充分不必要條件 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | {x|-2≤x<1} | B. | {x|-2≤x≤2} | C. | {x|1<x≤2} | D. | {x|x<2} |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com