
分析 (1)先求導,再分類討論,得到函數的單調區間;
(2)由題意,只要求出函數f(x)min>0即可,利用導數和函數的最值的關系,進行分類討論,即可得到a的范圍.
解答 解:(1)由f(x)=ax2+bx-lnx,x∈(0,+∞),得$f'(x)=\frac{{2a{x^2}+bx-1}}{x}$.
①當a=0時,$f'(x)=\frac{bx-1}{x}$.
(i) 若b≤0,當x>0時,f'(x)<0恒成立,所以函數f(x)的單調遞減區間是(0,+∞).
(ii) 若b>0,當$0<x<\frac{1}{b}$時,f'(x)<0,函數f(x)單調遞減.
當$x>\frac{1}{b}$時,f'(x)>0,函數f(x)單調遞增.
所以函數f(x)的單調遞減區間是$(0,\frac{1}{b})$,單調遞增區間是$(\frac{1}{b},+∞)$.
②當a>0時,令f'(x)=0,得2ax2+bx-1=0.
由△=b2+8a>0得${x_1}=\frac{{-b-\sqrt{{b^2}+8a}}}{4a},\;{x_2}=\frac{{-b+\sqrt{{b^2}+8a}}}{4a}$.
顯然,x1<0,x2>0.
當0<x<x2時,f'(x)<0,函數f(x)單調遞減.
當x>x2時,f'(x)>0,函數f(x)單調遞增.
所以函數f(x)的單調遞減區間是$(0,\frac{{-b+\sqrt{{b^2}+8a}}}{4a})$,單調遞增區間是$(\frac{{-b+\sqrt{{b^2}+8a}}}{4a},+∞)$.
綜上所述,
當a=0,b≤0時,函數f(x)的單調遞減區間是(0,+∞).
當a=0,b>0時,函數f(x)的單調遞減區間是$(0,\frac{1}{b})$,單調遞增區間是$(\frac{1}{b},+∞)$.
當a>0時,函數f(x)的單調遞減區間是$(0,\frac{{-b+\sqrt{{b^2}+8a}}}{4a})$,單調遞增區間是$(\frac{{-b+\sqrt{{b^2}+8a}}}{4a},+∞)$
(2)①當a=0時,b=-2,f(x)在(0,+∞)上單調遞減,f(1)=-2<0,不合題意.
②當a>0時,由(1)可知,f(x)在$(0,\frac{1}{a})$單調遞減,在$(\frac{1}{a},+∞)$上單調遞增,
所以只需f(x)的最小值為$f(\frac{1}{a})=a{(\frac{1}{a})^2}+(a-2)•\frac{1}{a}-ln\frac{1}{a}$=$lna-\frac{1}{a}+1>0$即可,
令$g(a)=lna-\frac{1}{a}+1$,
則g(a)在(0,+∞)上單調遞增,
g(1)=0,
所以當0<a<1時,g(a)<0,
當a>1時,g(a)>0,
所以a的取值范圍是(1,+∞).
點評 本題主要考查函數的單調性及最值,以及分類討論的思想,轉化思想,屬于中檔題.


 提分百分百檢測卷單元期末測試卷系列答案
提分百分百檢測卷單元期末測試卷系列答案 小學期末標準試卷系列答案
小學期末標準試卷系列答案科目:高中數學 來源: 題型:解答題
 在棱長為2的正方體ABCD-A1B1C1D1中,E,F分別為A1B1,CD的中點.
在棱長為2的正方體ABCD-A1B1C1D1中,E,F分別為A1B1,CD的中點.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{{3}^{2015}}{2}$+$\frac{3}{2}$ | B. | $\frac{{3}^{2015}}{8}$ | C. | $\frac{{3}^{2015}}{8}$+$\frac{3}{2}$ | D. | $\frac{{3}^{2015}}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
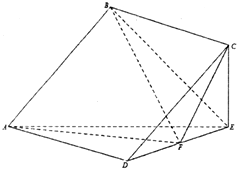 在幾何體ABCDE中,四邊形ABCD是正方形,CE⊥平面ADE且CE=EF=2,F是線段DE的中點.
在幾何體ABCDE中,四邊形ABCD是正方形,CE⊥平面ADE且CE=EF=2,F是線段DE的中點.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
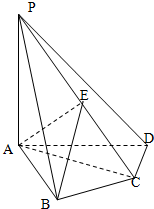 在四棱錐P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中點.
在四棱錐P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中點.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
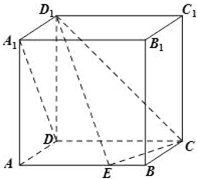 如圖,在棱長為1的正方體ABCD-A1B1C1D1中,點E是棱AB上的動點.
如圖,在棱長為1的正方體ABCD-A1B1C1D1中,點E是棱AB上的動點.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com