
���}Ŀ����֪�E�A![]() (
(![]() �酢��(sh��)),����һ�lֱ��,ʹ�ô�ֱ�����@Щ�E�A�صõľ����L(zh��ng)������
�酢��(sh��)),����һ�lֱ��,ʹ�ô�ֱ�����@Щ�E�A�صõľ����L(zh��ng)������![]() ,��ֱ������_____.
,��ֱ������_____.
���𰸡�![]()
��������
������E�A![]() (
(![]() �酢��(sh��))��ʾ������ֱ��
�酢��(sh��))��ʾ������ֱ��![]() �ϣ��L(zh��ng)�S�L(zh��ng)�Ͷ��S�L(zh��ng)�քe��4,2��һ�M�E�A���Д�����ϗl����ֱ����Ҫ�cֱ��
�ϣ��L(zh��ng)�S�L(zh��ng)�Ͷ��S�L(zh��ng)�քe��4,2��һ�M�E�A���Д�����ϗl����ֱ����Ҫ�cֱ��![]() ƽ�У��O(sh��)��ֱ�����̣�������һ��(g��)����ęE�A�cֱ������(li��n)�����ֱ���ķ��̣����C����(du��)�����еęE�A���M��l��.
ƽ�У��O(sh��)��ֱ�����̣�������һ��(g��)����ęE�A�cֱ������(li��n)�����ֱ���ķ��̣����C����(du��)�����еęE�A���M��l��.
��:�E�A![]() (
(![]() �酢��(sh��))�ɻ���
�酢��(sh��))�ɻ���![]() ��
��
����![]() ��ʾ������ֱ��
��ʾ������ֱ��![]() ��,�L(zh��ng)�S�L(zh��ng)�Ͷ��S�L(zh��ng)�քe��4,2��һ�M�E�A���������ֱ���c�@�M�E�A�N������E�A���ཻ��
��,�L(zh��ng)�S�L(zh��ng)�Ͷ��S�L(zh��ng)�քe��4,2��һ�M�E�A���������ֱ���c�@�M�E�A�N������E�A���ཻ��
�������ֱ��![]() �cֱ��
�cֱ��![]() ��ƽ�У��t�ض����ڙE�A�cֱ��
��ƽ�У��t�ض����ڙE�A�cֱ��![]() ���ཻ��
���ཻ��
���ǣ��O(sh��)����ֱ���ķ��̞�![]() ��
��
��?y��n)��ֱ�����@Щ�E�A�صõľ����L(zh��ng)������![]() ���tֱ��
���tֱ��![]() �c�E�A
�c�E�A![]() ���õ����L(zh��ng)��
���õ����L(zh��ng)��![]() ���O(sh��)�ҵăɶ��c(di��n)��
���O(sh��)�ҵăɶ��c(di��n)��![]() ��
��![]() ��
��
��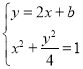 ��
��![]() ������
������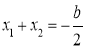 ��
��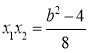 ��
��
����![]() ����
����![]() ��
��
���![]() ��
��
�O(sh��)ֱ��![]() �c�E�A
�c�E�A![]() (
(![]() �酢��(sh��))���ཻ���õ����L(zh��ng)��
�酢��(sh��))���ཻ���õ����L(zh��ng)��![]() ���ҵăɶ��c(di��n)�飺
���ҵăɶ��c(di��n)�飺![]() ��
��![]() ��
��
�t��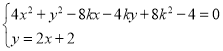 ��
��![]() ��
��
����![]() ��
��![]() ��
��
���![]()
����ֱ��![]() �c�E�A
�c�E�A![]() (
(![]() �酢��(sh��))�ཻ���õ����L(zh��ng)��
�酢��(sh��))�ཻ���õ����L(zh��ng)��![]() .
.
ͬ�����C,��(du��)����![]() ,�E�A
,�E�A![]() (
(![]() �酢��(sh��))�cֱ��
�酢��(sh��))�cֱ��![]() �ཻ�������L(zh��ng)��
�ཻ�������L(zh��ng)��![]() .
.


 ��ĩ�����Ԫ�z�y(c��)���(f��)��(x��)��ϵ�д�
��ĩ�����Ԫ�z�y(c��)���(f��)��(x��)��ϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����(sh��)��![]() ��ǰ
��ǰ![]() �(xi��ng)��ӛ��
�(xi��ng)��ӛ��![]() ��(du��)�����������(sh��)n��������������(sh��)m��ʹ��
��(du��)�����������(sh��)n��������������(sh��)m��ʹ��![]() ���t�Q
���t�Q![]() ����H��(sh��)������
����H��(sh��)������
��1������(sh��)��![]() ��ͨ�(xi��ng)��ʽ
��ͨ�(xi��ng)��ʽ![]() ���Д�
���Д�![]() �Ƿ����H��(sh��)������
�Ƿ����H��(sh��)������
��2���Ȳ(sh��)��![]() ������
������![]() ��
��![]() �����C��
�����C��![]() ����H��(sh��)������
����H��(sh��)������
��3���O(sh��)�c(di��n)![]() ��ֱ��
��ֱ��![]() �ϣ�����
�ϣ�����![]() ��
��![]() ����
����![]() ����H��(sh��)��������
����H��(sh��)��������![]() �M��ėl����
�M��ėl����
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ�����}��ʾ:����ABC��һ�K�돽��2ǧ�ף��A�ĽǞ�60�����L(f��ng)���^(q��)��P�c(di��n)�ڻ�BC�ϣ��F(xi��n)�����L(f��ng)���^(q��)��Ҏ(gu��)�����l���l�̘I(y��)�ֵ�PQ��QR��RP��Ҫ��ֵ�PQ�cAB��ֱ���ֵ�PR�cAC��ֱ��ֱ��PQ��ʾ�����l�ֵ���
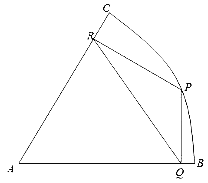
(1)���Pλ�ڻ�BC�����c(di��n)�������l�ֵ��Ŀ��L(zh��ng)�ȣ�
(2)���ڭh(hu��n)����ԭ�����l�ֵ�PQ��PR��QRÿ���ܮa(ch��n)���Ľ�(j��ng)��(j��)Ч��քe��ÿǧ��300�fԪ��200�fԪ��400�fԪ����:�@���l�ֵ�ÿ���ܮa(ch��n)���Ľ�(j��ng)��(j��)��Ч����ߞ���٣�(���_��1�fԪ)
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���O(sh��)�P(gu��n)��x�ķ���2x2��ax��2=0�ăɸ��քe������£������£�������(sh��)![]()
��1���C��f��x���څ^(q��)�g�������£�����������(sh��)��
��2����(d��ng)a���ֵ�r(sh��)��f��x���څ^(q��)�g[������]�ϵ����ֵ�c��Сֵ֮����С��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ�������������|(zh��)�ĺ���(sh��)�Q����![]() ����(sh��)�����ٶ��x��?y��n)?/span>
����(sh��)�����ٶ��x��?y��n)?/span>![]() ����
����![]() ���溯��(sh��)����
���溯��(sh��)����![]() ������(sh��)
������(sh��)![]() ������
������![]() ��
��![]() �φ��{(di��o)�f������(du��)����һ��(g��)С��
�φ��{(di��o)�f������(du��)����һ��(g��)С��![]() ������(sh��)
������(sh��)![]() �����ٴ���һ��(g��)��׃��
�����ٴ���һ��(g��)��׃��![]() ��ʹ
��ʹ![]() .�����Ă�(g��)����(sh��)��
.������(g��)����(sh��)��![]() ��
��![]() ��
�� ��
�� ����
����![]() ����(sh��)���Ă�(g��)��(sh��)�飨 ��
����(sh��)���Ă�(g��)��(sh��)�飨 ��
A.![]() ��(g��)B.
��(g��)B.![]() ��(g��)C.
��(g��)C.![]() ��(g��)D.
��(g��)D.![]() ��(g��)
��(g��)
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪�c(di��n)![]() �ǒ��タ
�ǒ��タ![]() ��
��![]() �Ľ��c(di��n)��ֱ��
�Ľ��c(di��n)��ֱ��![]() �c���タ
�c���タ![]() �������c(di��n)
�������c(di��n)![]() ���B��
���B��![]() �����タ����һ�c(di��n)
�����タ����һ�c(di��n)![]() ���^�c(di��n)
���^�c(di��n)![]() ��
��![]() �Ĵ��������タ
�Ĵ��������タ![]() ����һ�c(di��n)
����һ�c(di��n)![]() .
.
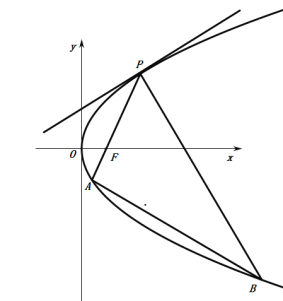
��1����![]() ����ֱ��
����ֱ��![]() �ķ��̣�
�ķ��̣�
��2����������![]() ��e
��e![]() ����Сֵ.
����Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���������}��
�ٺ���(sh��)![]() �ĈD���P(gu��n)��
�ĈD���P(gu��n)��![]() �S��(du��)�Q�ij�Ҫ�l����
�S��(du��)�Q�ij�Ҫ�l����![]() ��
��![]() ��
��
����֪![]() �ǵȲ(sh��)��
�ǵȲ(sh��)��![]() ��ǰ
��ǰ![]() �(xi��ng)�ͣ���
�(xi��ng)�ͣ���![]() ���t
���t![]() ��
��
�ۺ���(sh��)![]() �c����(sh��)
�c����(sh��)![]() �ĈD���P(gu��n)��ֱ��
�ĈD���P(gu��n)��ֱ��![]() ��(du��)�Q��
��(du��)�Q��
�܌�(du��)������ɗl����ֱ���������ڟo�F����(g��)ƽ���c�@�ɗl����ֱ�����ɵĽ����.
�������_�����}�� ��
A.1��(g��)B.2��(g��)C.3��(g��)D.4��(g��)
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���O(sh��)f(x)�Ƕ��x��R �����ڞ�1�ĺ���(sh��)���څ^(q��)�g![]() �ϣ�
�ϣ� ![]() ���м���D=
���м���D=![]() ���t����f(x)-lgx=0�Ľ�Ă�(g��)��(sh��)��____________
���t����f(x)-lgx=0�Ľ�Ă�(g��)��(sh��)��____________
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D����֪����![]() �У�
��![]() ��
��![]() ��
��![]() ����߅��
����߅��![]() ����Σ�
����Σ�![]() ��ƽ��
��ƽ��![]() ƽ��
ƽ��![]() ��
��

�������C��![]() ƽ��
ƽ��![]() ��
��
������ƽ��![]() �cƽ��
�cƽ��![]() �����J����ǵ�����ֵ��
�����J����ǵ�����ֵ��
�����ھ���![]() ���Ƿ�����c(di��n)
���Ƿ�����c(di��n)![]() ��ʹ��ֱ��
��ʹ��ֱ��![]() �cƽ��
�cƽ��![]() ���ɽǵ�����ֵ��
���ɽǵ�����ֵ��![]() �������ڣ��������
�������ڣ��������![]() ���L(zh��ng)���������ڣ�Ո(q��ng)�f�����ɣ�
���L(zh��ng)���������ڣ�Ո(q��ng)�f�����ɣ�
�鿴�𰸺ͽ���>>
�ٶ����� - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com