
【題目】如題所示:扇形ABC是一塊半徑為2千米,圓心角為60°的風景區,P點在弧BC上,現欲在風景區中規劃三條三條商業街道PQ、QR、RP,要求街道PQ與AB垂直,街道PR與AC垂直,直線PQ表示第三條街道。
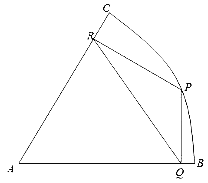
(1)如果P位于弧BC的中點,求三條街道的總長度;
(2)由于環境的原因,三條街道PQ、PR、QR每年能產生的經濟效益分別為每千米300萬元、200萬元及400萬元,問:這三條街道每年能產生的經濟總效益最高為多少?(精確到1萬元)
科目:高中數學 來源: 題型:
【題目】已知數列{an}為等差數列,a1=1,前n項和為Sn,數列{bn}為等比數列,b1>1,公比為2,且b2S3=54,b3+S2=16.
(Ⅰ)求數列{an}與{bn}的通項公式;
(Ⅱ)設數列{cn}滿足cn=an+bn,求數列{cn}的前n項和Tn.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校為了普及環保知識,增強學生的環保意識,在全校組織了一次有關環保知識的競賽.經過初賽、復賽,甲、乙兩個代表隊(每隊3人)進入了決賽,規定每人回答一個問題,答對為本隊贏得10分,答錯得0分.假設甲隊中每人答對的概率均為![]() ,乙隊中3人答對的概率分別為
,乙隊中3人答對的概率分別為![]() ,
,![]() ,
,![]() ,且各人回答正確與否相互之間沒有影響,用
,且各人回答正確與否相互之間沒有影響,用![]() 表示乙隊的總得分.
表示乙隊的總得分.
(Ⅰ)求![]() 的分布列及數學期望;
的分布列及數學期望;
(Ⅱ)求甲、乙兩隊總得分之和等于30分且甲隊獲勝的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(x)=log4(4x+1)+kx是偶函數.
(1)求k的值;
(2)判斷函數y=f(x)-![]() x在R上的單調性,并加以證明;
x在R上的單調性,并加以證明;
(3)設g(x)=log4(a2x-![]() a),若函數f(x)與g(x)的圖象有且僅有一個交點,求實數a的取值范圍.
a),若函數f(x)與g(x)的圖象有且僅有一個交點,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知![]() 是橢圓
是橢圓![]() 的左焦點,且橢圓
的左焦點,且橢圓![]() 經過點
經過點![]() .
.
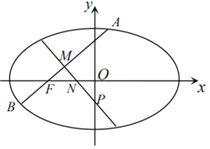
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)若過點![]() 的直線
的直線![]() 交橢圓
交橢圓![]() 于
于![]() 、
、![]() 兩點,線段
兩點,線段![]() 的中點為
的中點為![]() ,過
,過![]() 且與
且與![]() 垂直的直線與
垂直的直線與![]() 軸和
軸和![]() 軸分別交于
軸分別交于![]() 、
、![]() 兩點,記
兩點,記![]() 、
、![]() 的面積分別為
的面積分別為![]() 、
、![]() .若
.若![]() ,求直線
,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() ,
,![]() 滿足:
滿足:![]() .
.
(1)若![]() ,求數列
,求數列![]() 的通項公式;
的通項公式;
(2)若![]() ,且
,且![]() .
.
① 記![]() ,求證:數列
,求證:數列![]() 為等差數列;
為等差數列;
② 若數列![]() 中任意一項的值均未在該數列中重復出現無數次,求首項
中任意一項的值均未在該數列中重復出現無數次,求首項![]() 應滿足的條件.
應滿足的條件.
查看答案和解析>>
科目:高中數學 來源: 題型:
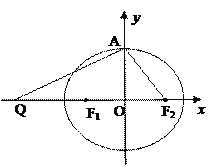
【題目】如圖,設橢圓![]() 的左、右焦點分別為F1,F2,上頂點為A,過點A與AF2垂直的直線交x軸負半軸于點Q,且
的左、右焦點分別為F1,F2,上頂點為A,過點A與AF2垂直的直線交x軸負半軸于點Q,且![]() 0,若過 A,Q,F2三點的圓恰好與直線
0,若過 A,Q,F2三點的圓恰好與直線![]() 相切,過定點 M(0,2)的直線
相切,過定點 M(0,2)的直線![]() 與橢圓C交于G,H兩點(點G在點M,H之間).(Ⅰ)求橢圓C的方程;(Ⅱ)設直線
與橢圓C交于G,H兩點(點G在點M,H之間).(Ⅰ)求橢圓C的方程;(Ⅱ)設直線![]() 的斜率
的斜率![]() ,在x軸上是否存在點P(
,在x軸上是否存在點P(![]() ,0),使得以PG,PH為鄰邊的平行四邊形是菱形?如果存在,求出
,0),使得以PG,PH為鄰邊的平行四邊形是菱形?如果存在,求出![]() 的取值范圍;如果不存在,請說明理由;(Ⅲ)若實數
的取值范圍;如果不存在,請說明理由;(Ⅲ)若實數![]() 滿足
滿足![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,
中,![]() ,
,![]() 是曲線段
是曲線段![]() :
:![]() (
(![]() 是參數,
是參數,![]() )的左、右端點,
)的左、右端點,![]() 是
是![]() 上異于
上異于![]() ,
,![]() 的動點,過點
的動點,過點![]() 作直線
作直線![]() 的垂線,垂足為
的垂線,垂足為![]() .
.
(1)建立適當的極坐標系,寫出點![]() 軌跡的極坐標方程;
軌跡的極坐標方程;
(2)求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com