
【題目】已知數列![]() ,
,![]() 滿足:
滿足:![]() .
.
(1)若![]() ,求數列
,求數列![]() 的通項公式;
的通項公式;
(2)若![]() ,且
,且![]() .
.
① 記![]() ,求證:數列
,求證:數列![]() 為等差數列;
為等差數列;
② 若數列![]() 中任意一項的值均未在該數列中重復出現無數次,求首項
中任意一項的值均未在該數列中重復出現無數次,求首項![]() 應滿足的條件.
應滿足的條件.
【答案】(1)![]()
(2)①根據等差數列的定義,證明相鄰兩項的差為定值來得到證明.從第二項起滿足題意即可.
②當![]()
![]() ,數列
,數列![]() 任意一項的值均未在該數列中重復出現無數次
任意一項的值均未在該數列中重復出現無數次
【解析】
試題解:(1)當![]() 時,有
時,有
![]() .
.
又![]() 也滿足上式,所以數列
也滿足上式,所以數列![]() 的通項公式是
的通項公式是![]() . 4分
. 4分
(2)①因為對任意的![]() ,有
,有![]() ,所以,
,所以,
![]() ,
,
所以,數列![]() 為等差數列. 8分
為等差數列. 8分
②設![]() (其中
(其中![]() 為常數且
為常數且![]() ,
,
所以,![]() ,
,
即數列![]() 均為以7為公差的等差數列. 10分
均為以7為公差的等差數列. 10分
設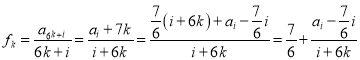 .
.
(其中![]() 為
為![]() 中一個常數)
中一個常數)
當![]() 時,對任意的
時,對任意的![]() ,有
,有![]() ; 12分
; 12分
當![]() 時,
時,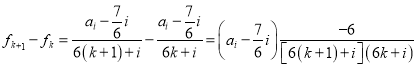 .
.
(Ⅰ)若![]() ,則對任意的
,則對任意的![]() 有
有![]() ,所以數列
,所以數列![]() 為遞減數列;
為遞減數列;
(Ⅱ)若![]() ,則對任意的
,則對任意的![]() 有
有![]() ,所以數列
,所以數列![]() 為遞增數列.
為遞增數列.
綜上所述,集合![]() .
.
當![]() 時,數列
時,數列![]() 中必有某數重復出現無數次;
中必有某數重復出現無數次;
當![]() 時,數列
時,數列![]() 均為單調數列,任意一個數在這6個數列中最多出現一次,所以數列
均為單調數列,任意一個數在這6個數列中最多出現一次,所以數列![]() 任意一項的值均未在該數列中重復出現無數次. 18分
任意一項的值均未在該數列中重復出現無數次. 18分


科目:高中數學 來源: 題型:
【題目】已知矩形![]() ,
,![]() ,
,![]() ,將
,將![]() 沿對角線
沿對角線![]() 進行翻折,得到三棱錐
進行翻折,得到三棱錐![]() ,則在翻折的過程中,有下列結論正確的有_____.
,則在翻折的過程中,有下列結論正確的有_____.
①三棱錐![]() 的體積的最大值為
的體積的最大值為![]() ;
;
②三棱錐![]() 的外接球體積不變;
的外接球體積不變;
③三棱錐![]() 的體積最大值時,二面角
的體積最大值時,二面角![]() 的大小是60°;
的大小是60°;
④異面直線![]() 與
與![]() 所成角的最大值為90°.
所成角的最大值為90°.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,
中,![]() 為坐標原點,C、D兩點的坐標為
為坐標原點,C、D兩點的坐標為![]() ,曲線
,曲線![]() 上的動點P滿足
上的動點P滿足![]() .又曲線
.又曲線![]() 上的點A、B滿足
上的點A、B滿足![]() .
.
(1)求曲線![]() 的方程;
的方程;
(2)若點A在第一象限,且![]() ,求點A的坐標;
,求點A的坐標;
(3)求證:原點到直線AB的距離為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如題所示:扇形ABC是一塊半徑為2千米,圓心角為60°的風景區,P點在弧BC上,現欲在風景區中規劃三條三條商業街道PQ、QR、RP,要求街道PQ與AB垂直,街道PR與AC垂直,直線PQ表示第三條街道。
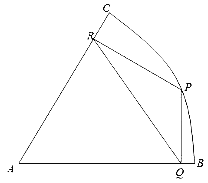
(1)如果P位于弧BC的中點,求三條街道的總長度;
(2)由于環境的原因,三條街道PQ、PR、QR每年能產生的經濟效益分別為每千米300萬元、200萬元及400萬元,問:這三條街道每年能產生的經濟總效益最高為多少?(精確到1萬元)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱錐![]() 中,
中,![]() 底面
底面![]() ,
,![]() .點
.點![]() 、
、![]() 、
、![]() 分別為棱
分別為棱![]() 、
、![]() 、
、![]() 的中點,
的中點,![]() 是線段
是線段![]() 的中點,
的中點,![]() ,
,![]() .
.
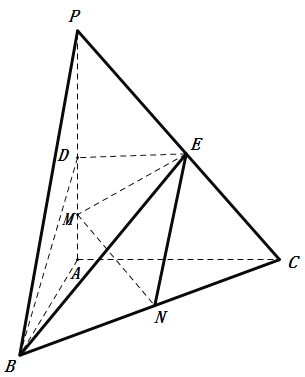
(1)求證:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的正弦值;
的正弦值;
(3)已知點![]() 在棱
在棱![]() 上,且直線
上,且直線![]() 與直線
與直線![]() 所成角的余弦值為
所成角的余弦值為![]() ,求線段
,求線段![]() 的長.
的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】![]() 年
年![]() 月,中國良渚古城遺址獲準列入世界遺產名錄,標志著中華五千年文明史得到國際社會認可.良渚古城遺址是人類早期城市文明的范例,實證了中華五千年文明史.考古科學家在測定遺址年齡的過程中利用了“放射性物質因衰變而減少”這一規律.已知樣本中碳
月,中國良渚古城遺址獲準列入世界遺產名錄,標志著中華五千年文明史得到國際社會認可.良渚古城遺址是人類早期城市文明的范例,實證了中華五千年文明史.考古科學家在測定遺址年齡的過程中利用了“放射性物質因衰變而減少”這一規律.已知樣本中碳![]() 的質量
的質量![]() 隨時間
隨時間![]() (單位:年)的衰變規律滿足
(單位:年)的衰變規律滿足![]() (
(![]() 表示碳
表示碳![]() 原有的質量),則經過
原有的質量),則經過![]() 年后,碳
年后,碳![]() 的質量變為原來的________;經過測定,良渚古城遺址文物樣本中碳
的質量變為原來的________;經過測定,良渚古城遺址文物樣本中碳![]() 的質量是原來的
的質量是原來的![]() 至
至![]() ,據此推測良渚古城存在的時期距今約在________年到
,據此推測良渚古城存在的時期距今約在________年到![]() 年之間.(參考數據:
年之間.(參考數據:![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
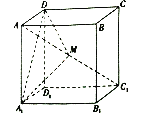
【題目】在棱長為2的正方體![]() 中,點
中,點![]() 是對角線
是對角線![]() 上的點(點
上的點(點![]() 與
與![]() 、
、![]() 不重合),則下列結論正確的個數為( )
不重合),則下列結論正確的個數為( )
①存在點![]() ,使得平面
,使得平面![]() 平面
平面![]() ;
;
②存在點![]() ,使得
,使得![]() 平面
平面![]() ;
;
③若![]() 的面積為
的面積為![]() ,則
,則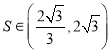 ;
;
④若![]() 、
、![]() 分別是
分別是![]() 在平面
在平面![]() 與平面
與平面![]() 的正投影的面積,則存在點
的正投影的面積,則存在點![]() ,使得
,使得![]() .
.
A.1個B.2個C.3個D.4個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com