
【題目】在平面直角坐標系![]() 中,
中,![]() 為坐標原點,C、D兩點的坐標為
為坐標原點,C、D兩點的坐標為![]() ,曲線
,曲線![]() 上的動點P滿足
上的動點P滿足![]() .又曲線
.又曲線![]() 上的點A、B滿足
上的點A、B滿足![]() .
.
(1)求曲線![]() 的方程;
的方程;
(2)若點A在第一象限,且![]() ,求點A的坐標;
,求點A的坐標;
(3)求證:原點到直線AB的距離為定值.
【答案】(1)![]() (2)
(2)![]() (3)證明見解析
(3)證明見解析
【解析】
(1)由![]() ,
,![]() 知,曲線
知,曲線![]() 是以
是以![]() 、
、![]() 為焦點,長軸
為焦點,長軸![]() 的橢圓,即可求曲線
的橢圓,即可求曲線![]() 的方程(2)設直線
的方程(2)設直線![]() 的方程為
的方程為![]() ,則直線
,則直線![]() 的方程為
的方程為![]() ,與橢圓方程聯立,由
,與橢圓方程聯立,由![]() 知
知![]() ,即可求點
,即可求點![]() 的坐標(3)分類討論,設直線
的坐標(3)分類討論,設直線![]() 的方程
的方程![]() ,與橢圓方程聯立,求出原點到直線
,與橢圓方程聯立,求出原點到直線![]() 的距離,即可證明原點到直線
的距離,即可證明原點到直線![]() 的距離為定值.
的距離為定值.
(1)由![]() ,
,![]() 知,曲線E是以C、D為焦點,長軸
知,曲線E是以C、D為焦點,長軸![]() 的橢圓,
的橢圓,
設其方程為![]() ,則有
,則有![]() ,
,
∴曲線E的方程為![]()
(2)設直線OA的方程為![]() ,則直線OB的方程為
,則直線OB的方程為![]()
由則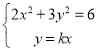 得
得![]() ,解得
,解得![]()
同理,由則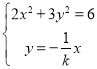 解得
解得![]() .
.
由![]() 知
知![]() ,
,
即![]()
解得![]() ,因點A在第一象限,故
,因點A在第一象限,故![]() ,
,
此時點A的坐標為![]()
(3)設![]() ,
,![]() ,
,
當直線AB平行于坐標軸時,由![]() 知A、B兩點之一為
知A、B兩點之一為![]() 與橢圓的交點,
與橢圓的交點,
由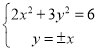
解得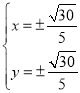 ,
,
此時原點到直線AB的距離為![]() ,
,
當直線AB不平行于坐標軸時,設直線AB的方程![]() ,
,
由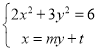 得
得![]()
由![]() 得
得![]()
即![]()
因![]()
代入得![]() 即
即![]()
原點到直線AB的距離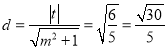 .
.


科目:高中數學 來源: 題型:
【題目】2019年10月18日-27日,第七屆世界軍人運動會在湖北武漢舉辦,中國代表團共獲得133金64銀42銅,共239枚獎牌.為了調查各國參賽人員對主辦方的滿意程度,研究人員隨機抽取了500名參賽運動員進行調查,所得數據如下所示,現有如下說法:①在參與調查的500名運動員中任取1人,抽到對主辦方表示滿意的男性運動員的概率為![]() ;②在犯錯誤的概率不超過1%的前提下可以認為“是否對主辦方表示滿意與運動員的性別有關”;③沒有99.9%的把握認為“是否對主辦方表示滿意與運動員的性別有關”;則正確命題的個數為( )附:
;②在犯錯誤的概率不超過1%的前提下可以認為“是否對主辦方表示滿意與運動員的性別有關”;③沒有99.9%的把握認為“是否對主辦方表示滿意與運動員的性別有關”;則正確命題的個數為( )附:
男性運動員 | 女性運動員 | |||||
對主辦方表示滿意 | 200 | 220 | ||||
對主辦方表示不滿意 | 50 | 30 | ||||
| 0.100 | 0.050 | 0.010 | 0.001 | ||
k | 2.706 | 3.841 | 6.635 | 10.828 | ||
A.0B.1C.2D.3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]()
![]() 的離心率為
的離心率為![]() ,
,![]() ,
,![]() 分別是橢圓的左右焦點,過點
分別是橢圓的左右焦點,過點![]() 的直線交橢圓于
的直線交橢圓于![]() ,
,![]() 兩點,且
兩點,且![]() 的周長為12.
的周長為12.
(Ⅰ)求橢圓![]() 的方程
的方程
(Ⅱ)過點![]() 作斜率為
作斜率為![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于兩點
交于兩點![]() ,
,![]() ,試判斷在
,試判斷在![]() 軸上是否存在點
軸上是否存在點![]() ,使得
,使得![]() 是以
是以![]() 為底邊的等腰三角形若存在,求點
為底邊的等腰三角形若存在,求點![]() 橫坐標的取值范圍,若不存在,請說明理由.
橫坐標的取值范圍,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為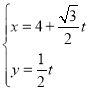 (
(![]() 為參數).以坐標原點為極點,
為參數).以坐標原點為極點,![]() 軸正半軸為極軸建立極坐標系,曲線
軸正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]()
(1)在曲線![]() 上任取一點
上任取一點![]() ,連接
,連接![]() ,在射線
,在射線![]() 上取一點
上取一點![]() ,使
,使![]() ,求
,求![]() 點軌跡的極坐標方程;
點軌跡的極坐標方程;
(2)在曲線![]() 上任取一點
上任取一點![]() ,在曲線
,在曲線![]() 上任取一點
上任取一點![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知![]() 為等邊三角形,
為等邊三角形,![]() 為等腰直角三角形,
為等腰直角三角形,![]() ,平面
,平面![]() 平面ABD,點E與點D在平面ABC的同側,且
平面ABD,點E與點D在平面ABC的同側,且![]() ,
,![]() .點F為AD中點,連接EF.
.點F為AD中點,連接EF.
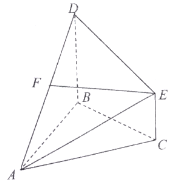
(1)求證:![]() 平面ABC;
平面ABC;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com