
【題目】某小學(xué)對五年級的學(xué)生進(jìn)行體質(zhì)測試,已知五年一班共有學(xué)生30人,測試立定跳遠(yuǎn)的成績用莖葉圖表示如圖(單位:![]() ):男生成績在175
):男生成績在175![]() 以上(包括175
以上(包括175![]() )定義為“合格”,成績在175
)定義為“合格”,成績在175![]() 以下(不包括175
以下(不包括175![]() )定義為“不合格”.女生成績在165
)定義為“不合格”.女生成績在165![]() 以上(包括165
以上(包括165![]() )定義為“合格”,成績在165
)定義為“合格”,成績在165![]() 以下(不包括165
以下(不包括165![]() )定義為“不合格”.
)定義為“不合格”.
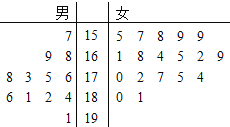
(1)求五年一班的女生立定跳遠(yuǎn)成績的中位數(shù);
(2)在五年一班的男生中任意選取3人,求至少有2人的成績是合格的概率;
(3)若從五年一班成績“合格”的學(xué)生中選取2人參加復(fù)試,用![]() 表示其中男生的人數(shù),寫出
表示其中男生的人數(shù),寫出![]() 的分布列,并求
的分布列,并求![]() 的數(shù)學(xué)期望.
的數(shù)學(xué)期望.
【答案】(1)166.5cm (2) ![]() (3)見解析
(3)見解析
【解析】
(1)按照中位數(shù)的定義,可以根據(jù)莖葉圖得到五年一班的女生立定跳遠(yuǎn)成績的中位數(shù);
(2) 男生中任意選取3人,至少有2人的成績是合格,包括兩個事件:一個為事件![]() :“僅有兩人的成績合格”,另一個為事件
:“僅有兩人的成績合格”,另一個為事件![]() :“有三人的成績合格”,所以至少有兩人的成績是合格的概率:
:“有三人的成績合格”,所以至少有兩人的成績是合格的概率:![]() ,分別求出
,分別求出![]() ,最后求出
,最后求出![]() ;
;
(3) 因?yàn)楹细竦娜斯灿?8人,其中有女生有10人合格,男生有8人合格,依題意,![]() 的取值為0,1,2,分別求出
的取值為0,1,2,分別求出![]() 的值,最后列出
的值,最后列出![]() 的分布列和計(jì)算出
的分布列和計(jì)算出![]() 的數(shù)學(xué)期望.
的數(shù)學(xué)期望.
解:(1)由莖葉圖得五年一班的女生立定跳遠(yuǎn)成績的中位數(shù)為![]()
(2)設(shè)“僅有兩人的成績合格”為事件![]() ,“有三人的成績合格”為事件
,“有三人的成績合格”為事件![]() ,
,
至少有兩人的成績是合格的概率:![]() ,
,
又男生共12人,其中有8人合格,從而![]() ,
,
![]() ,所以
,所以![]() .
.
(3)因?yàn)楹细竦娜斯灿?8人,其中有女生有10人合格,男生有8人合格,
依題意,![]() 的取值為0,1,2,
的取值為0,1,2,
則![]() ,
,
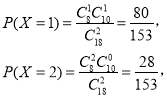
因此,X的分布列如下:
| 0 | 1 | 2 |
|
|
|
|
![]() (人).
(人).
或是,因?yàn)?/span>![]() 服從超幾何分布,所以
服從超幾何分布,所以![]() (人).
(人).


 海淀黃岡名師導(dǎo)航系列答案
海淀黃岡名師導(dǎo)航系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的焦距為
的焦距為![]() ,橢圓
,橢圓![]() 上任意一點(diǎn)到橢圓兩個焦點(diǎn)的距離之和為6.
上任意一點(diǎn)到橢圓兩個焦點(diǎn)的距離之和為6.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)設(shè)直線![]()
![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點(diǎn),點(diǎn)
兩點(diǎn),點(diǎn)![]() (0,1),且
(0,1),且![]() =
=![]() ,求直線
,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=(x﹣2)ex﹣![]() +
+![]() x,其中
x,其中![]() ∈R,e是自然對數(shù)的底數(shù).
∈R,e是自然對數(shù)的底數(shù).
(1)當(dāng)![]() >0時(shí),討論函數(shù)f(x)在(1,+∞)上的單調(diào)性;
>0時(shí),討論函數(shù)f(x)在(1,+∞)上的單調(diào)性;
(2)若函數(shù)g(x)=f![]() (x)+2﹣
(x)+2﹣![]() ,證明:使g(x)≥0在
,證明:使g(x)≥0在![]() 上恒成立的實(shí)數(shù)a能取到的最大整數(shù)值為1.
上恒成立的實(shí)數(shù)a能取到的最大整數(shù)值為1.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,其圖象關(guān)于直線
,其圖象關(guān)于直線![]() 對稱,為了得到函數(shù)
對稱,為了得到函數(shù)![]() 的圖象,只需將函數(shù)
的圖象,只需將函數(shù)![]() 的圖象上的所有點(diǎn)( )
的圖象上的所有點(diǎn)( )
A.先向左平移![]() 個單位長度,再把所得各點(diǎn)橫坐標(biāo)伸長為原來的2倍,縱坐標(biāo)保持不變
個單位長度,再把所得各點(diǎn)橫坐標(biāo)伸長為原來的2倍,縱坐標(biāo)保持不變
B.先向右平移![]() 個單位長度,再把所得各點(diǎn)橫坐標(biāo)縮短為原來的
個單位長度,再把所得各點(diǎn)橫坐標(biāo)縮短為原來的![]() ,縱坐標(biāo)保持不變
,縱坐標(biāo)保持不變
C.先向右平移![]() 個單位長度,再把所得各點(diǎn)橫坐標(biāo)伸長為原來的2倍,縱坐標(biāo)保持不變
個單位長度,再把所得各點(diǎn)橫坐標(biāo)伸長為原來的2倍,縱坐標(biāo)保持不變
D.先向左平移![]() 個單位長度,再把所得各點(diǎn)橫坐標(biāo)縮短為原來的
個單位長度,再把所得各點(diǎn)橫坐標(biāo)縮短為原來的![]() ,縱坐標(biāo)保持不變
,縱坐標(biāo)保持不變
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)數(shù)列![]() 的各項(xiàng)都是正數(shù),若對于任意的正整數(shù)
的各項(xiàng)都是正數(shù),若對于任意的正整數(shù)![]() ,存在
,存在![]() ,使得
,使得![]() 、
、![]() 、
、![]() 成等比數(shù)列,則稱函數(shù)
成等比數(shù)列,則稱函數(shù)![]() 為“
為“![]() 型”數(shù)列.
型”數(shù)列.
(1)若![]() 是“
是“![]() 型”數(shù)列,且
型”數(shù)列,且![]() ,
,![]() ,求
,求![]() 的值;
的值;
(2)若![]() 是“
是“![]() 型”數(shù)列,且
型”數(shù)列,且![]() ,
,![]() ,求
,求![]() 的前
的前![]() 項(xiàng)和
項(xiàng)和![]() ;
;
(3)若![]() 既是“
既是“![]() 型”數(shù)列,又是“
型”數(shù)列,又是“![]() 型”數(shù)列,求證:數(shù)列
型”數(shù)列,求證:數(shù)列![]() 是等比數(shù)列.
是等比數(shù)列.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,射線![]() 和
和![]() 均為筆直的公路,扇形
均為筆直的公路,扇形![]() 區(qū)域(含邊界)是一蔬菜種植園,其中
區(qū)域(含邊界)是一蔬菜種植園,其中![]() 、
、![]() 分別在射線
分別在射線![]() 和
和![]() 上.經(jīng)測量得,扇形
上.經(jīng)測量得,扇形![]() 的圓心角(即
的圓心角(即![]() )為
)為![]() 、半徑為1千米.為了方便菜農(nóng)經(jīng)營,打算在扇形
、半徑為1千米.為了方便菜農(nóng)經(jīng)營,打算在扇形![]() 區(qū)域外修建一條公路
區(qū)域外修建一條公路![]() ,分別與射線
,分別與射線![]() 、
、![]() 交于
交于![]() 、
、![]() 兩點(diǎn),并要求
兩點(diǎn),并要求![]() 與扇形弧
與扇形弧![]() 相切于點(diǎn)
相切于點(diǎn)![]() .設(shè)
.設(shè)![]() (單位:弧度),假設(shè)所有公路的寬度均忽略不計(jì).
(單位:弧度),假設(shè)所有公路的寬度均忽略不計(jì).
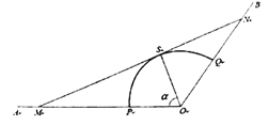
(1)試將公路![]() 的長度表示為
的長度表示為![]() 的函數(shù),并寫出
的函數(shù),并寫出![]() 的取值范圍;
的取值范圍;
(2)試確定![]() 的值,使得公路
的值,使得公路![]() 的長度最小,并求出其最小值.
的長度最小,并求出其最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
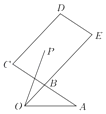
【題目】如圖,B是AC的中點(diǎn),![]() ,P是平行四邊形BCDE內(nèi)(含邊界)的一點(diǎn),且
,P是平行四邊形BCDE內(nèi)(含邊界)的一點(diǎn),且![]() .有以下結(jié)論:
.有以下結(jié)論:
①當(dāng)x=0時(shí),y∈[2,3];
②當(dāng)P是線段CE的中點(diǎn)時(shí),![]() ;
;
③若x+y為定值1,則在平面直角坐標(biāo)系中,點(diǎn)P的軌跡是一條線段;
④x﹣y的最大值為﹣1;
其中你認(rèn)為正確的所有結(jié)論的序號為_____.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com