
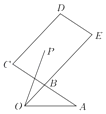
【題目】如圖,B是AC的中點,![]() ,P是平行四邊形BCDE內(含邊界)的一點,且
,P是平行四邊形BCDE內(含邊界)的一點,且![]() .有以下結論:
.有以下結論:
①當x=0時,y∈[2,3];
②當P是線段CE的中點時,![]() ;
;
③若x+y為定值1,則在平面直角坐標系中,點P的軌跡是一條線段;
④x﹣y的最大值為﹣1;
其中你認為正確的所有結論的序號為_____.
科目:高中數學 來源: 題型:
【題目】某小學對五年級的學生進行體質測試,已知五年一班共有學生30人,測試立定跳遠的成績用莖葉圖表示如圖(單位:![]() ):男生成績在175
):男生成績在175![]() 以上(包括175
以上(包括175![]() )定義為“合格”,成績在175
)定義為“合格”,成績在175![]() 以下(不包括175
以下(不包括175![]() )定義為“不合格”.女生成績在165
)定義為“不合格”.女生成績在165![]() 以上(包括165
以上(包括165![]() )定義為“合格”,成績在165
)定義為“合格”,成績在165![]() 以下(不包括165
以下(不包括165![]() )定義為“不合格”.
)定義為“不合格”.
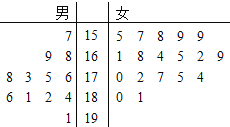
(1)求五年一班的女生立定跳遠成績的中位數;
(2)在五年一班的男生中任意選取3人,求至少有2人的成績是合格的概率;
(3)若從五年一班成績“合格”的學生中選取2人參加復試,用![]() 表示其中男生的人數,寫出
表示其中男生的人數,寫出![]() 的分布列,并求
的分布列,并求![]() 的數學期望.
的數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于實數![]() ,將滿足“
,將滿足“![]() 且
且![]() 為整數”的實數
為整數”的實數![]() 稱為實數
稱為實數![]() 的小數部分,用記號
的小數部分,用記號![]() 表示.對于實數
表示.對于實數![]() ,無窮數列
,無窮數列![]() 滿足如下條件:
滿足如下條件:![]() ,
,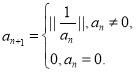 其中
其中![]() .
.
(1)若![]() ,求數列
,求數列![]() ;
;
(2)當![]() 時,對任意的
時,對任意的![]() ,都有
,都有![]() ,求符合要求的實數
,求符合要求的實數![]() 構成的集合
構成的集合![]() ;
;
(3)若![]() 是有理數,設
是有理數,設![]() (
(![]() 是整數,
是整數,![]() 是正整數,
是正整數,![]() 互質),問對于大于
互質),問對于大于![]() 的任意正整數
的任意正整數![]() ,是否都有
,是否都有![]() 成立,并證明你的結論.
成立,并證明你的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知無窮數列![]() 的前n項和為
的前n項和為![]() ,記
,記![]() ,
, ![]() ,…,
,…, ![]() 中奇數的個數為
中奇數的個數為![]() .
.
(Ⅰ)若![]() = n,請寫出數列
= n,請寫出數列![]() 的前5項;
的前5項;
(Ⅱ)求證:"![]() 為奇數,
為奇數, ![]() (i = 2,3,4,...)為偶數”是“數列
(i = 2,3,4,...)為偶數”是“數列![]() 是單調遞增數列”的充分不必要條件;
是單調遞增數列”的充分不必要條件;
(Ⅲ)若![]() ,i=1, 2, 3,…,求數列
,i=1, 2, 3,…,求數列![]() 的通項公式.
的通項公式.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}是以d為公差的等差數列,{bn}數列是以q為公比的等比數列.
(1)若數列{bn}的前n項和為Sn,且a1=b1=d=2,S3<a1003+5b2﹣2010,求整數q的值;
(2)在(1)的條件下,試問數列中是否存在一項bk,使得bk恰好可以表示為該數列中連續p(p∈N,p≥2)項的和?請說明理由;
(3)若b1=ar,b2=as≠ar,b3=at(其中t>s>r,且(s﹣r)是(t﹣r)的約數),求證:數列{bn}中每一項都是數列{an}中的項.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,以橢圓![]() (
(![]() )的右焦點
)的右焦點![]() 為圓心,
為圓心,![]() 為半徑作圓
為半徑作圓![]() (其中
(其中![]() 為已知橢圓的半焦距),過橢圓上一點
為已知橢圓的半焦距),過橢圓上一點![]() 作此圓的切線,切點為
作此圓的切線,切點為![]() .
.
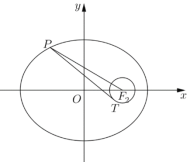
(1)若![]() ,
,![]() 為橢圓的右頂點,求切線長
為橢圓的右頂點,求切線長![]() ;
;
(2)設圓![]() 與
與![]() 軸的右交點為
軸的右交點為![]() ,過點
,過點![]() 作斜率為
作斜率為![]() (
(![]() )的直線
)的直線![]() 與橢圓相交于
與橢圓相交于![]() 、
、![]() 兩點,若
兩點,若![]() 恒成立,且
恒成立,且![]() .求:
.求:
(ⅰ)![]() 的取值范圍;
的取值范圍;
(ⅱ)直線![]() 被圓
被圓![]() 所截得弦長的最大值.
所截得弦長的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某溫室大棚規定,一天中,從中午12點到第二天上午8點為保溫時段,其余4小時為工作作業時段,從中午12點連續測量20小時,得出此溫室大棚的溫度y(單位:度)與時間t(單位:小時,![]() )近似地滿足函數
)近似地滿足函數![]() 關系,其中,b為大棚內一天中保溫時段的通風量。
關系,其中,b為大棚內一天中保溫時段的通風量。
(1)若一天中保溫時段的通風量保持100個單位不變,求大棚一天中保溫時段的最低溫度(精確到0.1℃);
(2)若要保持一天中保溫時段的最低溫度不小于17℃,求大棚一天中保溫時段通風量的最小值。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列1,1,1,2,2,1,2,4,3,1,2,4,8,4,1,2,4,8,16,5,…,其中第一項是![]() ,第二項是1,接著兩項為
,第二項是1,接著兩項為![]() ,
,![]() ,接著下一項是2,接著三項是
,接著下一項是2,接著三項是![]() ,
,![]() ,
,![]() ,接著下一項是3,依此類推.記該數列的前
,接著下一項是3,依此類推.記該數列的前![]() 項和為
項和為![]() ,則滿足
,則滿足![]() 的最小的正整數
的最小的正整數![]() 的值為( )
的值為( )
A.65B.67C.75D.77
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com