
| A. | [-$\frac{\sqrt{3}}{3}$,0] | B. | [-$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{3}}{3}$] | C. | [0,$\frac{\sqrt{3}}{3}$] | D. | (-∞,$\frac{\sqrt{3}}{3}$] |
分析 曲線的參數方程消去參數,將曲線C先化為普通方程,然后再結合圖形計算,由此能求出$\frac{y}{x}$的取值范圍.
解答 解:∵曲線$\left\{\begin{array}{l}x=-2+cosθ\\ y=sinθ\end{array}$(0≤θ<π,θ是參數),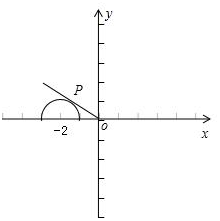
∴曲線C的普通方程為(x+2)2+y2=1(y≥0),
∴曲線C是以點C(-2,0)為圓心半徑為1的上半圓,
設點P(x,y)為曲線C上一動點,
則 $\frac{y}{x}$=kOP,(6分)
當P的坐標為(-$\frac{3}{2}$,$\frac{\sqrt{3}}{2}$)時,$\frac{y}{x}$有最小值為-$\frac{\sqrt{3}}{3}$,
當P的坐標為(-1,0)時,$\frac{y}{x}$有最大值為0,
∴$\frac{y}{x}$的取值范圍是[-$\frac{\sqrt{3}}{3}$,0].
故選:A.
點評 本題考查參數方程與普通方程的區別和聯系,兩者要會互相轉化,根據實際情況選擇不同的方程進行求解,考查運算求解能力,考查數形結合思想、化歸與轉化思想.屬于中檔題.


 習題精選系列答案
習題精選系列答案科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\overrightarrow{a}$∥$\overrightarrow{b}$ | B. | $\overrightarrow{a}$⊥$\overrightarrow{b}$ | C. | $\overrightarrow{a}$∥$\overrightarrow{c}$或$\overrightarrow{b}$∥$\overrightarrow{c}$ | D. | $\overrightarrow{a}$⊥$\overrightarrow{c}$或$\overrightarrow{b}$⊥$\overrightarrow{c}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
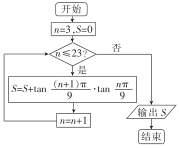
| A. | $-\frac{{2\sqrt{3}}}{{tan\frac{π}{9}}}-21$ | B. | $\frac{{tan\frac{25π}{9}-\sqrt{3}}}{{tan\frac{π}{9}}}-22$ | ||
| C. | $-\frac{{2\sqrt{3}}}{{tan\frac{π}{9}}}-22$ | D. | $\frac{{tan\frac{25π}{9}-\sqrt{3}}}{{tan\frac{π}{9}}}-21$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
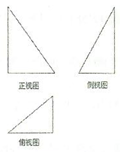
| A. | $\sqrt{6}π$ | B. | $\frac{4}{3}π$ | C. | 4π | D. | 6π |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 充分不必要條件 | B. | 必要不充分條件 | ||
| C. | 充分必要條件 | D. | 既不充分也不必要條件 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com