
【題目】已知三個關于x的不等式:①![]() ;②
;②![]() ;③
;③![]()
(1)分別求出①和②的解集;
(2)若同時滿足①和②的x值也滿足③,求m的取值范圍;
(3)若同時滿足③的x至少滿足①和②的一個,求m的取值范圍.
【答案】(1)①的解集為![]() ;②的解集為
;②的解集為![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)由![]() 可知
可知![]() ,將此不等式與兩邊平方后的不等式聯立
,將此不等式與兩邊平方后的不等式聯立![]() ,解不等式組即可。(2)同時滿足①和②的x值為
,解不等式組即可。(2)同時滿足①和②的x值為![]() ,也滿足③,進而由不等式
,也滿足③,進而由不等式![]() 在
在![]() 時恒成立,求字母m的取值范圍即可。(3)由同時滿足③的x至少滿足①和②的一個,可得不等式
時恒成立,求字母m的取值范圍即可。(3)由同時滿足③的x至少滿足①和②的一個,可得不等式![]() 在
在![]() 或
或![]() 上恒成立,構造函數求字母m的取值范圍即可。
上恒成立,構造函數求字母m的取值范圍即可。
(1)不等式![]() 等價于
等價于![]() ,即
,即![]() ,所以
,所以![]() ,所以,不等式
,所以,不等式![]() 的解集為
的解集為![]() ;由
;由![]() 得
得![]() ,所以
,所以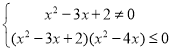 ,所以,
,所以,![]() 或
或![]() ,所以,不等式
,所以,不等式 ![]() 的解集為
的解集為![]() 。
。
(2)同時滿足①和②的x值為![]() 。由同時滿足①和②的x值也滿足③,可得
。由同時滿足①和②的x值也滿足③,可得![]() 在
在![]() 時恒成立。令
時恒成立。令![]() ,因為
,因為![]() ,所以
,所以![]() ,解得
,解得![]() 。所以, m的取值范圍為
。所以, m的取值范圍為![]() 。
。
(3)令![]() ,由已知條件可得
,由已知條件可得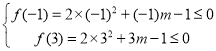 或
或![]() ,解得
,解得![]() ,所以,m的取值范圍為
,所以,m的取值范圍為![]() 。
。


 激活思維智能訓練課時導學練系列答案
激活思維智能訓練課時導學練系列答案科目:高中數學 來源: 題型:
【題目】已知△ABC的三個內角A,B,C所對的邊分別是a,b,c,向量![]() =(cos B,cos C),
=(cos B,cos C),![]() =(2a+c,b),且
=(2a+c,b),且![]() ⊥
⊥![]() .
.
(1)求角B的大小;
(2)若b=![]() ,求a+c的范圍.
,求a+c的范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地某高中2018年的高考考生人數是2015年高考考生人數的1.5倍.為了更好地對比該校考生的升學情況,統計了該校2015和2018年高考情況,得到如下餅圖:

2018年與2015年比較,下列結論正確的是( )
A. 一本達線人數減少
B. 二本達線人數增加了0.5倍
C. 藝體達線人數相同
D. 不上線的人數有所增加
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】圖一是美麗的“勾股樹”,它是一個直角三角形分別以它的每一邊向外作正方形而得到.圖二是第1代“勾股樹”,重復圖二的作法,得到圖三為第2代“勾股樹”,以此類推,已知最大的正方形面積為1,則第![]() 代“勾股樹”所有正方形的個數與面積的和分別為( )
代“勾股樹”所有正方形的個數與面積的和分別為( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知某運動員每次投籃命中的概率低于![]() ,現采用隨機模擬的方法估計該運動員三次投籃恰有兩次命中的概率:先由計算器產生0到9之間取整數值的隨機數,指定1,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三個隨機數為一組,代表三次投籃的結果,經隨機模擬產生了如下20組隨機數:
,現采用隨機模擬的方法估計該運動員三次投籃恰有兩次命中的概率:先由計算器產生0到9之間取整數值的隨機數,指定1,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三個隨機數為一組,代表三次投籃的結果,經隨機模擬產生了如下20組隨機數:
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
據此估計,該運動員三次投籃恰有兩次命中的概率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近年來,隨著科學技術迅猛發展,國內有實力的企業紛紛進行海外布局,如在智能手機行業,國產品牌已在趕超國外巨頭,某品牌手機公司一直默默拓展海外市場,在海外設多個分支機構需要國內公司外派大量80后、90后中青年員工.該企業為了解這兩個年齡層員工對是否愿意接受外派工作的態度隨機調查了100位員工,得到數據如下表:
愿意接受外派人數 | 不愿意接受外派人數 | 合計 | |
80后 | 20 | 20 | 40 |
90后 | 40 | 20 | 60 |
合計 | 60 | 40 | 100 |
(Ⅰ)根據調查的數據,判斷能否在犯錯誤的概率不超過0.1的前提下認為“是否愿意接受外派與年齡層有關”,并說明理由;
(Ⅱ)該公司選派12人參觀駐海外分支機構的交流體驗活動,在參與調查的80后員工中用分層抽樣方法抽出6名,組成80后組,在參與調查的90后員工中,也用分層抽樣方法抽出6名,組成90后組
①求這12 人中,80后組90后組愿意接受外派的人數各有多少?
②為方便交流,在80后組、90后組中各選出3人進行交流,記在80后組中選到愿意接受外派的人數為![]() ,在90 后組中選到愿意接受外派的人數為
,在90 后組中選到愿意接受外派的人數為![]() ,求
,求![]() 的概率.
的概率.
參考數據:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
參考公式:![]() ,其中
,其中![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com