
已知函數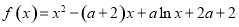 (其中
(其中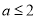 ).
).
(1)求函數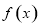 的單調區間;
的單調區間;
(2)若函數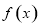 在
在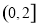 上有且只有一個零點,求實數
上有且只有一個零點,求實數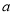 的取值范圍.
的取值范圍.
(1)詳見解析;(2)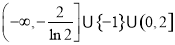 .
.
【解析】
試題分析:(1)先求函數 的定義域與導數
的定義域與導數 ,對
,對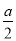 是否在定義域內以及在定義域內與
是否在定義域內以及在定義域內與 進行大小比較,從而確定函數的單調區間;(2)在(1)的條件下結合函數的單調性與零點存在定理對端點值或極值的正負進行限制,從而求出參數
進行大小比較,從而確定函數的單調區間;(2)在(1)的條件下結合函數的單調性與零點存在定理對端點值或極值的正負進行限制,從而求出參數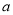 的取值范圍.
的取值范圍.
試題解析:(1)函數定義域為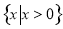 ,
,
 ,
,
①當 ,即
,即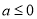 時,
時,
令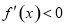 ,得
,得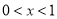 ,函數
,函數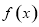 的單調遞減區間為
的單調遞減區間為 ,
,
令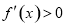 ,得
,得 ,函數
,函數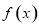 的單調遞增區間為
的單調遞增區間為 ;
;
②當 ,即
,即 時,
時,
令 ,得
,得 或
或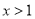 ,函數
,函數 的單調遞增區間為
的單調遞增區間為 ,
, ,
,
令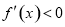 ,得
,得 ,函數
,函數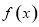 的單調遞減區間為
的單調遞減區間為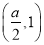 ;
;
③當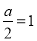 ,即
,即 時,
時, 恒成立,函數
恒成立,函數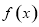 的單調遞增區間為
的單調遞增區間為 ;
;
(2)①當 時,由(1)可知,函數
時,由(1)可知,函數 的單調遞減區間為
的單調遞減區間為 ,
,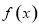 在
在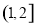 單調遞增,
單調遞增,
所以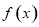 在
在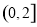 上的最小值為
上的最小值為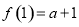 ,
,
由于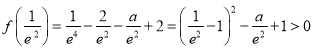 ,
,
要使 在
在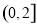 上有且只有一個零點,
上有且只有一個零點,
需滿足 或
或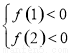 ,解得
,解得 或
或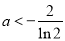 ,
,
所以當 或
或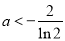 時,
時,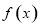 在
在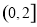 上有且只有一個零點;
上有且只有一個零點;
②當 時,由(1)可知,函數
時,由(1)可知,函數 在
在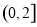 上單調遞增,
上單調遞增,
且 ,
,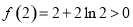 ,
,
所以當 時,
時, 在
在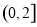 上有且只有一個零點;
上有且只有一個零點;
③當 時,由(1)可知,函數
時,由(1)可知,函數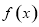 在
在 內單調遞增,在
內單調遞增,在 上單調遞減,在
上單調遞減,在 上單調遞增,
上單調遞增,
又因為 ,所以當
,所以當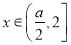 時,總有
時,總有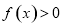 ,
,
因為 ,
,
所以 ,
,
所以 在區間
在區間 內必有零點,
內必有零點,
又因為 在
在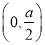 內單調遞增,
內單調遞增,
從而當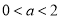 時,
時,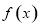 在
在 上有且只有一個零點,
上有且只有一個零點,
綜上所述,當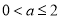 或
或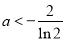 或
或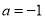 時,
時, 在
在 上有且只有一個零點.
上有且只有一個零點.
考點:1.函數的單調區間與導數;2.分類討論;3.函數的零點;4.零點存在定理


 期末沖刺100分創新金卷完全試卷系列答案
期末沖刺100分創新金卷完全試卷系列答案科目:高中數學 來源:2013-2014學年廣東省肇慶市高三3月第一次模擬理科數學試卷(解析版) 題型:選擇題
下列命題中,真命題是 ( )
A. ,
,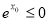 ;
;
B.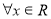 ,
,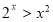 ;
;
C.“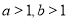 ”是“
”是“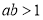 ”的充分不必要條件;
”的充分不必要條件;
D.設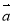 ,
,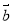 為向量,則“
為向量,則“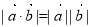 ”是“
”是“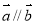 ”的必要不充分條件
”的必要不充分條件
查看答案和解析>>
科目:高中數學 來源:2013-2014學年廣東省湛江市高三高考模擬測試二理科數學試卷(解析版) 題型:選擇題
對于任意兩個正整數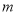 、
、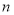 ,定義某種運算“※”,法則如下:當
,定義某種運算“※”,法則如下:當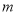 、
、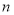 都是正奇數時,
都是正奇數時,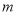 ※
※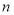 =
=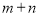 ;當
;當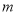 、
、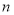 不全為正奇數時,
不全為正奇數時,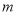 ※
※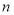 =
=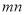 .則在此定義下,集合
.則在此定義下,集合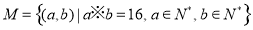 中的元素個數是( )
中的元素個數是( )
A.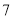 B.
B.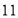 C.
C.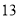 D.
D.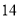
查看答案和解析>>
科目:高中數學 來源:2013-2014學年廣東省湛江市高三高考模擬測試二文科數學試卷(解析版) 題型:填空題
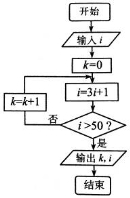
閱讀如圖所示的程序框圖,若輸入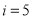 ,則輸出的
,則輸出的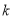 值為______________.
值為______________.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年廣東省汕頭市高三3月高考模擬考試文科試卷(解析版) 題型:解答題
某工廠生產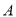 、
、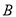 兩種元件,其質量按測試指標劃分為:大于或等于
兩種元件,其質量按測試指標劃分為:大于或等于 為正品,小于
為正品,小于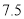 為次品.現從一批產品中隨機抽取這兩種元件各
為次品.現從一批產品中隨機抽取這兩種元件各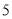 件進行檢測,檢測結果記錄如下:
件進行檢測,檢測結果記錄如下:
|
|
|
|
|
|
B |
|
|
|
|
|
由于表格被污損,數據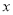 、
、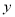 看不清,統計員只記得
看不清,統計員只記得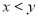 ,且
,且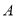 、
、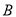 兩種元件的檢測數據的平均值相等,方差也相等.
兩種元件的檢測數據的平均值相等,方差也相等.
(1)求表格中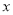 與
與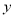 的值;
的值;
(2)從被檢測的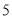 件
件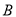 種元件中任取
種元件中任取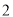 件,求
件,求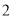 件都為正品的概率.
件都為正品的概率.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年廣東省汕頭市高三3月高考模擬考試文科試卷(解析版) 題型:選擇題
“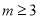 ”是“關于
”是“關于 、
、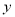 的不等式組
的不等式組 表示的平面區域為三角形”的( )
表示的平面區域為三角形”的( )
A.充分不必要條件 B.必要不充分條件
C.充要條件 D.既不充分也不必要條件
查看答案和解析>>
科目:高中數學 來源:2013-2014學年廣東省梅州市高三3月總復習質檢理科數學試卷(解析版) 題型:填空題
已知函數f(x)=x-[x],其中[x]表示不超過實數x的最大整數,若關于x的方程f(x)=kx+k有三個不同的實根,則實數k的取值范圍是__________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com