
| A. | (-2019,-2016) | B. | (-2019,2016) | C. | (-2019,+∞) | D. | (-∞,-2019) |
分析 通過觀察2f(x)+xf′(x)>x2,不等式的左邊像一個函數的導數,又直接寫不出來,對該不等式兩邊同乘以x,得到2xf(x)+x2f′(x)<x3,這時不等式的左邊是(x2f(x))′,所以構造函數F(x)=x2f(x),則能判斷該函數在(-∞,0)上是減函數;
再由F(x+2016)=(x+2016)2f(x+2016),F(-3)=9f(-3),且不等式(x+2016)2f(x+2016)-9f(-3)<0可變成F(x+2014)<F(-3),解這個不等式即可,這個不等式利用F(x)的單調性可以求解.
解答 解:由2f(x)+xf′(x)>x2,(x<0);
得:2xf(x)+x2f′(x)<x3,
即[x2f(x)]′<x3<0;
令F(x)=x2f(x);
則當x<0時,F'(x)<0,即F(x)在(-∞,0)上是減函數;
∴F(x+2016)=(x+2016)2f(x+2016),F(-3)=9f(-3);
即不等式等價為F(x+2016)-F(-3)<0;
∵F(x)在(-∞,0)是減函數;
∴由F(x+2016)<F(-3)得,x+2016>-3,∴x>-2019;
又x+2016<0,∴x<-2016;
∴-2019<x<-2016.
∴原不等式的解集是(-2019,-2016).
故選:A.
點評 本題考查函數的單調性與導數的關系,兩個函數乘積的導數的求法,而構造函數是解本題的關鍵.


科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 5,4 | B. | 5,3 | C. | 3,5 | D. | 4,5 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
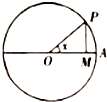 如圖,圓O的半徑為1,A是圓上的定點,P是圓上的動點,角x的始邊為射線OA,終邊為射線OP,過點P作直線OA的垂線,垂足為M,將點M到直線OP的距離與O到M的距離之和表示成x的函數f(x),則y=f(x)在[0,π]上的圖象大致是( )
如圖,圓O的半徑為1,A是圓上的定點,P是圓上的動點,角x的始邊為射線OA,終邊為射線OP,過點P作直線OA的垂線,垂足為M,將點M到直線OP的距離與O到M的距離之和表示成x的函數f(x),則y=f(x)在[0,π]上的圖象大致是( )| A. | 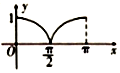 | B. | 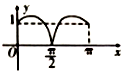 | C. | 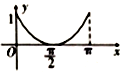 | D. | 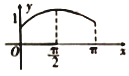 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 4 | B. | 3 | C. | $\frac{3}{2}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com