【題目】選修4-4：坐標系與參數方程
以直角坐標系的原點
為極點，
軸的正半軸為極軸，且兩個坐標系取相等的長度單位，
已知曲線
的參數方程為
（
為參數），曲線
的極坐標方程為
.曲線的圖象與軸、
軸分別交于
兩點.
（1）判斷兩點與曲線的位置關系；
（2）點
是曲線上異于兩點的動點，求
面積的最大值.
一線名師提優試卷系列答案
陽光試卷單元測試卷系列答案科目：高中數學 來源： 題型：
【題目】設橢圓
的右焦點為
，右頂點為
.已知
，其中
為原點， 
為橢圓的離心率.
（1）求橢圓的方程及離心率
的值；
（2）設過點
的直線
與橢圓交于點
（
不在
軸上），垂直于
的直線與
交于點
，與
軸交于點
.若
，且
，求直線
的斜率的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】從某企業生產的某種產品中抽取100件，測量這些產品的一項質量指標值，由測量結果得如下頻率分布直方圖：
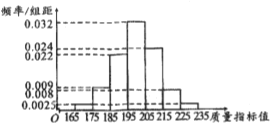
（1）求這100件產品質量指標值的樣本平均數
和樣本方差
（同一組的數據用該組區間的中點值作為代表）；
（2）由直方圖可以認為，這種產品的質量指標值
服從正態分布
，其中
近似為樣本平均數，
近似為樣本方差。
（i）若某用戶從該企業購買了10件這種產品，記
表示這10件產品中質量指標值位于（187.4，225.2）的產品件數，求
；
（ii）一天內抽取的產品中，若出現了質量指標值在
之外的產品，就認為這一天的生產過程中可能出現了異常情況，需對當天的生產過程進行檢查下。下面的莖葉圖是檢驗員在一天內抽取的15個產品的質量指標值，根據近似值判斷是否需要對當天的生產過程進行檢查。
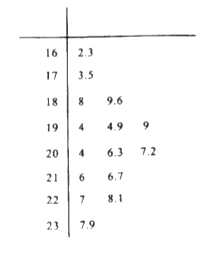
附：
，
，
，
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某市勞動部門堅持就業優先，釆取多項措施加快發展新興產業，服務經濟，帶來大量就業崗位，據政府工作報告顯示，截至2018年末，全市城鎮新增就業21.9萬人，創歷史新高．城鎮登記失業率為4.2%，比上年度下降0.73個百分點，處于近20年來的最低水平．
（1）現從該城鎮適齡人群中抽取100人，得到如下列聯表：
失業 | 就業 | 合計 | |
男 | 3 | 62 | 65 |
女 | 2 | 33 | 35 |
合計 | 5 | 95 | 100 |
根據聯表判斷是否有99%的把握認為失業與性別有關？
附：
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
（2）調查顯示，新增就業人群中，新興業態，民營經濟，大型國企對就業支撐作用不斷增強，其崗位比例為2∶5∶3，現要抽取一個樣本容量為50的樣本，則這三種崗位應該各抽取多少人？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在直角坐標系xOy中，已知直線l1的參數方程為
（t為參數），直線l2的參數方程為
（t為參數），其中α∈（0，
），以原點O為點x軸的非負半軸為極軸，取相同的單位長度建立極坐標系，曲線C的極坐標方程為ρ﹣2sinθ＝0．
（1）寫出直線l1的極坐標方程和曲線C的直角坐標方程；
（2）設直線l1，l2分別與曲線C交于點A，B（非坐標原點）求|AB|的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在直角坐標坐標系
中，曲線
的參數方程為
（
為參數），曲線
： 
.以
為極點， 
軸的非負半軸為極軸，與直角坐標系
取相同的長度單位，建立極坐標系.
（1）求曲線
的極坐標方程；
（2）射線
（
）與曲線
的異于極點的交點為
，與曲線
的交點為
，求
.
【答案】(1) 
的極坐標方程為
， 
的極坐標方程為
；(2) 
.
【解析】試題分析：（1）先根據三角函數平方關系消參數得曲線
，再根據
將曲線
的
極坐標方程；（2）將
代人曲線
的極坐標方程，再根據
求
.
試題解析：（1）曲線
的參數方程
（
為參數）
可化為普通方程
，
由
，可得曲線
的極坐標方程為
，
曲線
的極坐標方程為
.
（2）射線
（
）與曲線
的交點
的極徑為
，
射線
（
）與曲線
的交點
的極徑滿足
，解得
，
所以
.
【題型】解答題
【結束】
23
【題目】設函數
．
（1）設
的解集為
，求集合；
（2）已知
為（1）中集合中的最大整數，且
（其中
，
，
為正實數），求證：
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在直角坐標系
中，曲線
的參數方程為
為參數且
，
，
，曲線
的參數方程為
為參數），以
為極點，
軸正半軸為極軸建立極坐標系，曲線
的極坐標方程為
．
（1）求的普通方程及的直角坐標方程；
（2）若曲線與曲線
分別交于點
，
，求
的最大值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
