
【題目】已知集合![]() ,
,![]() ,集合
,集合 ,且集合
,且集合![]() 滿(mǎn)足
滿(mǎn)足![]() ,
,![]() .
.
(1)求實(shí)數(shù)![]() 的值;
的值;
(2)對(duì)集合![]() ,其中
,其中![]() ,定義由
,定義由![]() 中的元素構(gòu)成兩個(gè)相應(yīng)的集合:
中的元素構(gòu)成兩個(gè)相應(yīng)的集合:![]() ,
,![]() ,其中
,其中![]() 是有序數(shù)對(duì),集合
是有序數(shù)對(duì),集合![]() 和
和![]() 中的元素個(gè)數(shù)分別為
中的元素個(gè)數(shù)分別為![]() 和
和![]() ,若對(duì)任意的
,若對(duì)任意的![]() ,總有
,總有![]() ,則稱(chēng)集合
,則稱(chēng)集合![]() 具有性質(zhì)
具有性質(zhì)![]() .
.
①請(qǐng)檢驗(yàn)集合![]() 與
與![]() 是否具有性質(zhì)
是否具有性質(zhì)![]() ,并對(duì)其中具有性質(zhì)
,并對(duì)其中具有性質(zhì)![]() 的集合,寫(xiě)出相應(yīng)的集合
的集合,寫(xiě)出相應(yīng)的集合![]() 和
和![]() ;
;
②試判斷![]() 和
和![]() 的大小關(guān)系,并證明你的結(jié)論.
的大小關(guān)系,并證明你的結(jié)論.
【答案】(1)![]() (2)①
(2)①![]() 不具有性質(zhì)
不具有性質(zhì)![]() ,
,![]() 具有性質(zhì)
具有性質(zhì)![]() ;
;![]() ,
,![]() ②
②![]() ,證明見(jiàn)解析
,證明見(jiàn)解析
【解析】
(1)先求得集合![]() 所包含的元素,根據(jù)
所包含的元素,根據(jù)![]() ,
,![]() ,求得
,求得![]() 的值.
的值.
(2)根據(jù)(1)求得![]() ,由此求得
,由此求得![]() .
.
①根據(jù)性質(zhì)![]() 的定義,判斷出
的定義,判斷出![]() 不具有性質(zhì)
不具有性質(zhì)![]() ,
,![]() 具有性質(zhì)
具有性質(zhì)![]() .根據(jù)集合
.根據(jù)集合![]() 的定義求得
的定義求得![]() .
.
②根據(jù)①所求![]() ,求得
,求得![]() ,由此比較出兩者的大小關(guān)系.
,由此比較出兩者的大小關(guān)系.
(1)對(duì)于集合![]() ,
,![]() 開(kāi)口向下,對(duì)稱(chēng)軸為
開(kāi)口向下,對(duì)稱(chēng)軸為![]() ,當(dāng)
,當(dāng)![]() 時(shí)
時(shí)![]() ,故
,故![]()
對(duì)于集合![]() ,由
,由![]() ,解得
,解得![]() ,所以
,所以![]() .
.
根據(jù)題意![]() ,
,![]() ,所以
,所以![]() ,解得
,解得![]() 或
或![]() ,
,
經(jīng)檢驗(yàn),![]() 不符合
不符合![]() ,故舍去,
,故舍去,![]() 滿(mǎn)足題意,即
滿(mǎn)足題意,即![]() .
.
(2)由(1)得![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
①![]() 中
中![]() ,故
,故![]() 不具有性質(zhì)
不具有性質(zhì)![]() ;
;
![]() 中任意元素
中任意元素![]() ,故
,故![]() 具有性質(zhì)
具有性質(zhì)![]() ;根據(jù)集合
;根據(jù)集合![]() 的定義,求得
的定義,求得![]() ,
,![]() ;
;
②由①知,![]() ,故
,故![]() .
.


 小學(xué)數(shù)學(xué)口算題卡脫口而出系列答案
小學(xué)數(shù)學(xué)口算題卡脫口而出系列答案 優(yōu)秀生應(yīng)用題卡口算天天練系列答案
優(yōu)秀生應(yīng)用題卡口算天天練系列答案 浙江之星課時(shí)優(yōu)化作業(yè)系列答案
浙江之星課時(shí)優(yōu)化作業(yè)系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)函數(shù)![]() ,
, ![]() .
.
(1)解方程![]() .
.
(2)令![]() ,求
,求![]() 的值.
的值.
(3)若![]() 是定義在
是定義在![]() 上的奇函數(shù),且
上的奇函數(shù),且![]() 對(duì)任意
對(duì)任意![]() 恒成立,求實(shí)數(shù)k的取值范圍.
恒成立,求實(shí)數(shù)k的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某地有一企業(yè)2007年建廠并開(kāi)始投資生產(chǎn),年份代號(hào)為7,2008年年份代號(hào)為8,依次類(lèi)推.經(jīng)連續(xù)統(tǒng)計(jì)9年的收入情況如下表(經(jīng)數(shù)據(jù)分析可用線性回歸模型擬合![]() 與
與![]() 的關(guān)系):
的關(guān)系):
年份代號(hào)( | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
當(dāng)年收入( | 13 | 14 | 18 | 20 | 21 | 22 | 24 | 28 | 29 |
(Ⅰ)求![]() 關(guān)于
關(guān)于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(Ⅱ)試預(yù)測(cè)2020年該企業(yè)的收入.
(參考公式: 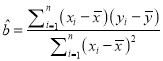
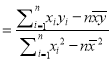 ,
, ![]() )
)
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在△OAB中,頂點(diǎn)A的坐標(biāo)是(3,0),頂點(diǎn)B的坐標(biāo)是(1,2),記△OAB位于直線![]() 左側(cè)圖形的面積為f(t).
左側(cè)圖形的面積為f(t).

(1)求函數(shù)f(t)的解析式;
(2)設(shè)函數(shù)![]() ,求函數(shù)
,求函數(shù)![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知圓![]() :
:![]() 與直線
與直線![]() :
:![]() ,動(dòng)直線
,動(dòng)直線![]() 過(guò)定點(diǎn)
過(guò)定點(diǎn)![]() .
.

(1)若直線![]() 與圓
與圓![]() 相切,求直線
相切,求直線![]() 的方程;
的方程;
(2)若直線![]() 與圓
與圓![]() 相交于
相交于![]() 、
、![]() 兩點(diǎn),點(diǎn)M是PQ的中點(diǎn),直線
兩點(diǎn),點(diǎn)M是PQ的中點(diǎn),直線![]() 與直線
與直線![]() 相交于點(diǎn)N.探索
相交于點(diǎn)N.探索![]() 是否為定值,若是,求出該定值;若不是,請(qǐng)說(shuō)明理由.
是否為定值,若是,求出該定值;若不是,請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)集合![]() ,若
,若![]() 是
是![]() 的子集,把
的子集,把![]() 中的所有數(shù)的和稱(chēng)為
中的所有數(shù)的和稱(chēng)為![]() 的“容量”(規(guī)定空集的容量為0),若
的“容量”(規(guī)定空集的容量為0),若![]() 的容量為奇(偶)數(shù),則稱(chēng)
的容量為奇(偶)數(shù),則稱(chēng)![]() 為
為![]() 的奇(偶)子集,命題①:
的奇(偶)子集,命題①:![]() 的奇子集與偶子集個(gè)數(shù)相等;命題②:當(dāng)
的奇子集與偶子集個(gè)數(shù)相等;命題②:當(dāng)![]() 時(shí),
時(shí),![]() 的所有奇子集的容量之和與所有偶子集的容量之和相等,則下列說(shuō)法正確的是( )
的所有奇子集的容量之和與所有偶子集的容量之和相等,則下列說(shuō)法正確的是( )
A.命題①和命題②都成立B.命題①和命題②都不成立
C.命題①成立,命題②不成立D.命題①不成立,命題②成立
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() ;
;
(1)討論![]() 的極值點(diǎn)的個(gè)數(shù);
的極值點(diǎn)的個(gè)數(shù);
(2)若![]() ,且
,且![]() 恒成立,求
恒成立,求![]() 的最大值.
的最大值.
參考數(shù)據(jù):
| 1.6 | 1.7 | 1.8 |
| 4.953 | 5.474 | 6.050 |
| 0.470 | 0.531 | 0.588 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)函數(shù)![]() ,其中
,其中![]() ,
,![]() .
.
(1)當(dāng)![]() 時(shí),討論函數(shù)
時(shí),討論函數(shù)![]() 的單調(diào)性;
的單調(diào)性;
(2)若函數(shù)![]() 僅在
僅在![]() 處有極值,求
處有極值,求![]() 的取值范圍;
的取值范圍;
(3)若對(duì)于任意的![]() ,不等式
,不等式![]() 在
在![]() 上恒成立,求
上恒成立,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知橢圓![]() 的右焦點(diǎn)為
的右焦點(diǎn)為![]() ,過(guò)
,過(guò)![]() 的直線
的直線![]() 與
與![]() 交于
交于![]() ,
,![]() 兩點(diǎn),點(diǎn)
兩點(diǎn),點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為![]() .當(dāng)
.當(dāng)![]() 軸時(shí),
軸時(shí),![]() 的面積為
的面積為![]() .
.
(1)求橢圓![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
(2)設(shè)直線![]() 、
、![]() 的斜率分別為
的斜率分別為![]() 、
、![]() ,證明:
,證明:![]() .
.
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com