
分析 模擬函數圖象的周期性,可判斷①;根據垂直平分線的幾何特征,可判斷②;根據回歸直線的實際意義,可判斷③;根據演繹推理及正弦函數的定義,可判斷④.
解答 解:若函數y=f(x)滿足f(x-1)=f(x+1),則函數f(x)是周期為2的周期函數,但不一定具有對稱性,故①錯誤;
點(2,1),(0,3)確定的直線斜率為-1,與直線x-y+1=0垂直,且中點(1,2)在直線x-y+1=0上,故點(2,1),(0,3)關于直線x-y+1=0的對稱,故②正確;
通過回歸方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$可以估計和觀測變量的取值和變化趨勢,故③正確;
正弦函數是奇函數,f(x)=sin(x2+1)是正弦函數,所以f(x)=sin(x2+1)是奇函數,上述推理錯誤的原因是小前提不正確,故④錯誤.
故答案為;②③
點評 本題以命題的真假判斷與應用為載體,考查了函數的對稱性,點的對稱變換,回歸分析,演繹推理等知識點,難度中檔.


 口算題卡加應用題集訓系列答案
口算題卡加應用題集訓系列答案 綜合自測系列答案
綜合自測系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
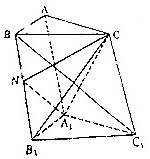 如圖,在直三棱柱ABC-A1B1 C1中,AC=2$\sqrt{2}$,AB=BC=BB1=2,N是BB1的中點.
如圖,在直三棱柱ABC-A1B1 C1中,AC=2$\sqrt{2}$,AB=BC=BB1=2,N是BB1的中點.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
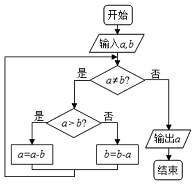 下面程序框圖的算法思路源于我國古代數學名著《九章算術》中的“更相減損術”.執行該程序框圖,若輸入的a,b分別為8,12,則輸出的a=( )
下面程序框圖的算法思路源于我國古代數學名著《九章算術》中的“更相減損術”.執行該程序框圖,若輸入的a,b分別為8,12,則輸出的a=( )| A. | 2 | B. | 0 | C. | 4 | D. | 16 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com