
分析 (1)利用同角三角函數的基本關系化簡要求的式子為sinα+cosα,從而得到答案.
(2)利用同角三角函數關系證得左邊=右邊=$\frac{(1+si{n}^{2}α)(1+co{s}^{2}α)}{co{s}^{2}α}$.
解答 證明:(1)$\frac{1-co{s}^{2}α}{sinα-cosα}$-$\frac{sinα+cosα}{ta{n}^{2}α-1}$=$\frac{si{n}^{2}α}{sinα-cosα}$-$\frac{co{s}^{2}α(sinα+cosα)}{si{n}^{2}α-co{s}^{2}α}$=$\frac{si{n}^{2}α}{sinα-cosα}$-$\frac{co{s}^{2}α}{sinα-cosα}$=sinα+cosα,
即左邊=右邊,
得證.
(2)左邊=(1+1-cos2α)(2+$\frac{si{n}^{2}α}{co{s}^{2}α}$)=(1+sin2α)$•\frac{co{s}^{2}+co{s}^{2}α+si{n}^{2}α}{co{s}^{2}α}$=$\frac{(1+si{n}^{2}α)(1+co{s}^{2}α)}{co{s}^{2}α}$.
右邊=(1+$\frac{2si{n}^{2}α}{co{s}^{2}α}$)(1+cos2α)=$\frac{co{s}^{2}α+si{n}^{2}α+si{n}^{2}α}{co{s}^{2}α}$(1+cos2α)=$\frac{(1+si{n}^{2}α)(1+co{s}^{2}α)}{co{s}^{2}α}$.
所以左邊=右邊.
得證.
點評 本題考查三角函數的化簡和證明,考查同角的基本關系式的運用,考查運算能力,屬于基礎題.


科目:高中數學 來源: 題型:選擇題
| A. | “a<b”是“am2<bm2”的充要條件 | |
| B. | 命題“?x∈R,x3-x2-1≤0”的否定是“?x∈R,x3-x2-1≤0” | |
| C. | “若 a,b都是奇數,則 a+b是偶數”的逆否命題是“若 a+b不是偶數,則 a,b不都是奇數” | |
| D. | 若 p∧q為假命題,則 p,q均為假命題 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
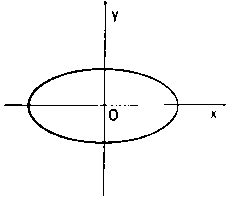 已知焦點在x軸上的橢圓C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{3}$=1,其離心率為$\frac{1}{2}$,過橢圓左焦點F1與上頂點B的直線為l0.
已知焦點在x軸上的橢圓C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{3}$=1,其離心率為$\frac{1}{2}$,過橢圓左焦點F1與上頂點B的直線為l0.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{10}$ | B. | $\frac{{\sqrt{10}}}{10}$ | C. | $\frac{{3\sqrt{10}}}{10}$ | D. | $\frac{9}{10}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
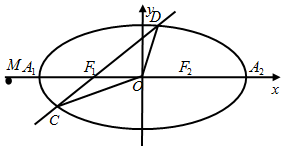 (文科)如圖,已知橢圓的中心在坐標原點,焦點F1,F2,在x軸上,長軸A1A2的長為4,x軸上一點M(${-\frac{a^2}{c},0}$),$|{\overrightarrow{M{A_1}}}|$=$2|{\overrightarrow{{A_1}{F_1}}}|$.
(文科)如圖,已知橢圓的中心在坐標原點,焦點F1,F2,在x軸上,長軸A1A2的長為4,x軸上一點M(${-\frac{a^2}{c},0}$),$|{\overrightarrow{M{A_1}}}|$=$2|{\overrightarrow{{A_1}{F_1}}}|$.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com