
分析 根據(jù)題意,由正弦函數(shù)的性質(zhì)分析可得:y=sinx上存在點(x0,y0),可得y0=sinx0∈[-1,1].函數(shù)f(x)=ex+2x-a在[-1,1]上單調(diào)遞增.利用函數(shù)f(x)的單調(diào)性可以證明f(y0)=y0.令函數(shù)f(x)=ex+2x-a=x,化為a=ex+x.令g(x)=ex+x (x∈[-1,1]).利用導(dǎo)數(shù)研究其單調(diào)性即可得出.
解答 解:曲線y=sinx上存在點(x0,y0),
∴y0=sinx0∈[-1,1].
函數(shù)f(x)=ex+2x-a在[-1,1]上單調(diào)遞增.
下面證明f(y0)=y0.
假設(shè)f(y0)=c>y0,則f(f(y0))=f(c)>f(y0)=c>y0,不滿足f(f(y0))=y0.
同理假設(shè)f(y0)=c<y0,則不滿足f(f(y0))=y0.
綜上可得:f(y0)=y0.
令函數(shù)f(x)=ex+2x-a=x,化為a=ex+x.
令g(x)=ex+x(x∈[-1,1]).
g′(x)=ex+1>0,∴函數(shù)g(x)在x∈[-1,1]單調(diào)遞增.
∴e-1-1≤g(x)≤e+1.
∴a的取值范圍是[-1+e-1,e+1];
故答案為:[-1+e-1,e+1].
點評 本題考查利用導(dǎo)數(shù)研究函數(shù)的單調(diào)性,涉及正弦函數(shù)的圖象和性質(zhì),關(guān)鍵是將原問題轉(zhuǎn)化為f(x)=x在[-1,1]上有解的問題.


科目:高中數(shù)學(xué) 來源: 題型:選擇題
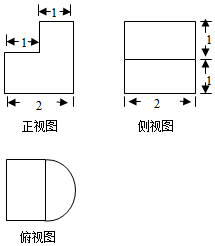
| A. | $\frac{1}{2}+\frac{π}{2}$ | B. | $1+\frac{π}{2}$ | C. | 1+π | D. | 2+π |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
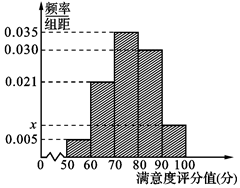 共享單車是指由企業(yè)在校園、公交站點、商業(yè)區(qū)、公共服務(wù)區(qū)等場所提供的自行車單車共享服務(wù),由于其依托“互聯(lián)網(wǎng)+”,符合“低碳出行”的理念,已越來越多地引起了人們的關(guān)注.某部門為了對該城市共享單車加強(qiáng)監(jiān)管,隨機(jī)選取了100人就該城市共享單車的推行情況進(jìn)行問卷調(diào)查,并將問卷中的這100人根據(jù)其滿意度評分值(百分制)按照 分成5組,制成如圖所示頻率分直方圖.
共享單車是指由企業(yè)在校園、公交站點、商業(yè)區(qū)、公共服務(wù)區(qū)等場所提供的自行車單車共享服務(wù),由于其依托“互聯(lián)網(wǎng)+”,符合“低碳出行”的理念,已越來越多地引起了人們的關(guān)注.某部門為了對該城市共享單車加強(qiáng)監(jiān)管,隨機(jī)選取了100人就該城市共享單車的推行情況進(jìn)行問卷調(diào)查,并將問卷中的這100人根據(jù)其滿意度評分值(百分制)按照 分成5組,制成如圖所示頻率分直方圖.查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
 已知函數(shù)f(x)是定義在R上的奇函數(shù),當(dāng)x>0時,f(x)=2x-3.
已知函數(shù)f(x)是定義在R上的奇函數(shù),當(dāng)x>0時,f(x)=2x-3.查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com