
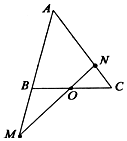
 如圖,在△ABC中,點O是BC的中點,過點O的直線分別交直線AB、AC于不同的兩點M、N,若$\overrightarrow{AM}=m\overrightarrow{AB}$,$\overrightarrow{AN}=n\overrightarrow{AC}({mn>0})$,則m+n的取值范圍為[2,+∞).
如圖,在△ABC中,點O是BC的中點,過點O的直線分別交直線AB、AC于不同的兩點M、N,若$\overrightarrow{AM}=m\overrightarrow{AB}$,$\overrightarrow{AN}=n\overrightarrow{AC}({mn>0})$,則m+n的取值范圍為[2,+∞). 分析 由三點共線時,以任意點為起點,這三點為終點的三向量,其中一向量可用另外兩向量線性表示,其系數和為1得到$\frac{1}{2m}$+$\frac{1}{2n}$=1,然后利用基本不等式求最值
解答 解:∵△ABC中,點O是BC的中點,
∴$\overrightarrow{AO}$=$\frac{1}{2}$($\overrightarrow{AB}$+$\overrightarrow{AC}$),
∵$\overrightarrow{AM}=m\overrightarrow{AB}$,$\overrightarrow{AN}=n\overrightarrow{AC}({mn>0})$,
∴$\overrightarrow{AO}$=$\frac{1}{2m}$$\overrightarrow{AM}$+$\frac{1}{2n}$$\overrightarrow{AN}$,
又∵O,M,N三點共線,
∴$\frac{1}{2m}$+$\frac{1}{2n}$=1,
∴m+n=$\frac{1}{2}$(m+n)($\frac{1}{m}$+$\frac{1}{n}$)=$\frac{1}{2}$(2+$\frac{n}{m}$+$\frac{m}{n}$)≥$\frac{1}{2}$(2+2$\sqrt{\frac{m}{n}•\frac{n}{m}}$)=2,當且僅當m=n=1時取等號,
故m+n的取值范圍為[2,+∞),
故答案為:[2,+∞)
點評 本題考查了共線向量基本定理的應用,考查了利用基本不等式求最值,關鍵是“1”的用法,是中檔題.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 函數值由負到正且為增函數 | B. | 函數值恒為正且為減函數 | ||
| C. | 函數值由正到負且為減函數 | D. | 沒有單調性 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | $\frac{3}{2}$ | C. | $\sqrt{2}$ | D. | -1 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 3 | B. | $\frac{25}{3}$或 3 | C. | $\sqrt{5}$ | D. | $\frac{{5\sqrt{15}}}{3}$或$\sqrt{15}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
 在正方體ABCD-A1B1C1D1中,E,F,G分別為A1B1,BB1,B1C1的中點,則AC1
在正方體ABCD-A1B1C1D1中,E,F,G分別為A1B1,BB1,B1C1的中點,則AC1查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (4,-2,7) | B. | (4,-1,7) | C. | (3,-1,7) | D. | (3,-2,7) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com