
【題目】在極坐標系下,已知圓O:ρ=cosθ+sinθ和直線l:![]() .
.
(1)求圓O和直線l的直角坐標方程;
(2)當θ∈(0,π)時,求直線l與圓O公共點的極坐標.
【答案】(1)x﹣y+1=0.(2)![]()
【解析】
試題(1)圓O的方程即ρ2=ρcosθ+ρsinθ,可得圓O 的直角坐標方程為:x2+y2=x+y,即x2+y2﹣x﹣y=0.
(2)由![]() ,可得直線l與圓O公共點的直角坐標為(0,1),由此求得線l與圓O公共點的極坐標.
,可得直線l與圓O公共點的直角坐標為(0,1),由此求得線l與圓O公共點的極坐標.
解:(1)圓O:ρ=cosθ+sinθ,即ρ2=ρcosθ+ρsinθ,
故圓O 的直角坐標方程為:x2+y2=x+y,即x2+y2﹣x﹣y=0.
直線l:![]() ,即ρsinθ﹣ρcosθ=1,則直線的直角坐標方程為:y﹣x=1,即x﹣y+1=0.
,即ρsinθ﹣ρcosθ=1,則直線的直角坐標方程為:y﹣x=1,即x﹣y+1=0.
(2)由![]() ,可得
,可得![]() ,直線l與圓O公共點的直角坐標為(0,1),
,直線l與圓O公共點的直角坐標為(0,1),
故直線l 與圓O 公共點的一個極坐標為![]() .
.


 通城學典默寫能手系列答案
通城學典默寫能手系列答案科目:高中數學 來源: 題型:
【題目】記![]() 是定義在
是定義在![]() 上且滿足如下條件的函數
上且滿足如下條件的函數![]() 組成的集合:
組成的集合:
①對任意的![]() ,都有
,都有![]() ;
;
②存在常數![]() ,使得對任意的
,使得對任意的![]() 、
、![]() ,都有
,都有![]() .
.
(1)設函數![]() ,
,![]() ,判斷函數
,判斷函數![]() 是否屬于
是否屬于![]() ?并說明理由;
?并說明理由;
(2)已知函數![]() ,求證:方程
,求證:方程![]() 的解至多一個;
的解至多一個;
(3)設函數![]() ,
,![]() ,且
,且![]() ,試求實數
,試求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(1)閱讀以下案例,利用此案例的想法化簡![]() .
.
案例:考察恒等式![]() 左右兩邊
左右兩邊![]() 的系數.
的系數.
因為右邊![]() ,
,
所以,右邊![]() 的系數為
的系數為![]() ,
,
而左邊![]() 的系數為
的系數為![]() ,
,
所以![]() =
=![]() .
.
(2)求證:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系xOy中,圓C1和C2的參數方程分別是![]() (φ為參數)和
(φ為參數)和![]() (φ為參數),以O為極點,x軸的正半軸為極軸建立極坐標系.
(φ為參數),以O為極點,x軸的正半軸為極軸建立極坐標系.
(1)求圓C1和C2的極坐標方程;
(2)射線OM:θ=a與圓C1的交點為O、P,與圓C2的交點為O、Q,求|OP||OQ|的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為迎接2022年北京冬季奧運會,普及冬奧知識,某校開展了“冰雪答題王”冬奧知識競賽活動.現從參加冬奧知識競賽活動的學生中隨機抽取了100名學生,將他們的比賽成績(滿分為100分)分為6組:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,得到如圖所示的頻率分布直方圖.
,得到如圖所示的頻率分布直方圖.
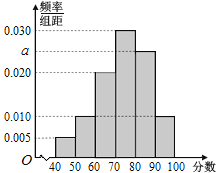
(1)求![]() 的值;
的值;
(2)估計這100名學生的平均成績(同一組中的數據用該組區間的中點值為代表);
(3)在抽取的100名學生中,規定:比賽成績不低于80分為“優秀”,比賽成績低于80分為“非優秀”.請將下面的2×2列聯表補充完整,并判斷是否有99.9%的把握認為“比賽成績是否優秀與性別有關”?
優秀 | 非優秀 | 合計 | |
男生 | 40 | ||
女生 | 50 | ||
合計 | 100 |
參考公式及數據:![]()
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 是橢圓
是橢圓![]() 的兩個焦點,
的兩個焦點,![]() 是橢圓
是橢圓![]() 上一點,當
上一點,當![]() 時,有
時,有![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)設過橢圓右焦點![]() 的動直線
的動直線![]() 與橢圓交于
與橢圓交于![]() 兩點,試問在
兩點,試問在![]() 鈾上是否存在與
鈾上是否存在與![]() 不重合的定點
不重合的定點![]() ,使得
,使得![]() 恒成立?若存在,求出定點
恒成立?若存在,求出定點![]() 的坐標,若不存在,請說明理由.
的坐標,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“回文數”是指從左到右與從右到左讀都一樣的正整數,如22,121,3553等.顯然2位“回文數”共9個:11,22,33,…,99.現從9個不同2位“回文數”中任取1個乘以4,其結果記為X;從9個不同2位“回文數”中任取2個相加,其結果記為Y.
(1)求X為“回文數”的概率;
(2)設隨機變量![]() 表示X,Y兩數中“回文數”的個數,求
表示X,Y兩數中“回文數”的個數,求![]() 的概率分布和數學期望
的概率分布和數學期望![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在對某漁業產品的質量調研中,從甲、乙兩地出產的該產品中各隨機抽取10件,測量該產品中某種元素的含量(單位:毫克).下表是測量數據的莖葉圖:
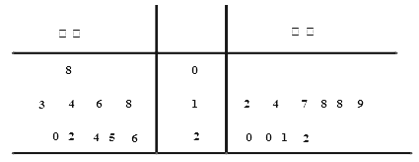
規定:當產品中的此種元素含量![]() 毫克時為優質品.
毫克時為優質品.
(1)試用上述樣本數據估計甲、乙兩地該產品的優質品率(優質品件數/總件數);
(2)從乙地抽出的上述10件產品中,隨機抽取3件,求抽到的3件產品中優質品數![]() 的分布列及數學期望
的分布列及數學期望![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com