
【題目】已知![]() 是橢圓
是橢圓![]() 的兩個焦點,
的兩個焦點,![]() 是橢圓
是橢圓![]() 上一點,當
上一點,當![]() 時,有
時,有![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)設過橢圓右焦點![]() 的動直線
的動直線![]() 與橢圓交于
與橢圓交于![]() 兩點,試問在
兩點,試問在![]() 鈾上是否存在與
鈾上是否存在與![]() 不重合的定點
不重合的定點![]() ,使得
,使得![]() 恒成立?若存在,求出定點
恒成立?若存在,求出定點![]() 的坐標,若不存在,請說明理由.
的坐標,若不存在,請說明理由.
【答案】(1)![]()
(2)存在, T(4,0)
【解析】
(1)由題意,![]() .故
.故![]() .然后設點
.然后設點![]() 坐標為
坐標為![]() ,代入橢圓方程,聯立橢圓定義
,代入橢圓方程,聯立橢圓定義![]() ,進一步計算可得橢圓
,進一步計算可得橢圓![]() 的標準方程;
的標準方程;
(2)假設存在與![]() 不重合的定點
不重合的定點![]() ,使得
,使得![]() 恒成立,則
恒成立,則![]() ,設出
,設出![]() 、
、![]() 、
、![]() 點坐標代入
點坐標代入![]() 計算,可得
計算,可得![]() .然后設直線
.然后設直線![]() .聯立直線與橢圓方程,消去
.聯立直線與橢圓方程,消去![]() 整理可得一元二次方程,根據韋達定理有
整理可得一元二次方程,根據韋達定理有![]() ,
,![]() .然后代入
.然后代入![]() 進行計算可判斷是否是定值,即可得到結論.
進行計算可判斷是否是定值,即可得到結論.
解:(1)由題意,![]() .故
.故![]() .
.
可設點![]() 坐標為
坐標為![]() ,則
,則
![]() ,解得
,解得![]() ,即
,即![]() .
.
![]() ,解得
,解得![]() .
.
![]() ,
,![]() .
.
![]() 橢圓
橢圓![]() 的標準方程為
的標準方程為![]() .
.
(2)由題意,假設存在與![]() 不重合的定點
不重合的定點![]() ,使得
,使得![]() 恒成立,
恒成立,
設![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,則
,則
![]() ,
,![]() .
.
![]() ,
,
![]() ,即
,即![]() .
.
整理,得![]() .
.
設直線![]() .
.
聯立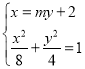 ,
,
消去![]() ,整理得
,整理得![]() .
.
![]()
![]() ,
,![]() .
.
![]()
![]() .
.
![]()
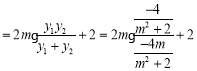
![]() .
.
![]() 存在與
存在與![]() 不重合的定點
不重合的定點![]() ,使得
,使得![]() 恒成立,且點
恒成立,且點![]() 坐標為
坐標為![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】已知等比數列![]() 的前n項和為
的前n項和為![]() ,且當
,且當![]() 時,
時,![]() 是
是![]() 與2m的等差中項
與2m的等差中項![]() 為實數
為實數![]() .
.
(1)求m的值及數列![]() 的通項公式;
的通項公式;
(2)令![]() ,是否存在正整數k,使得
,是否存在正整數k,使得![]() 對任意正整數n均成立?若存在,求出k的最大值;若不存在,說明理由.
對任意正整數n均成立?若存在,求出k的最大值;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在極坐標系下,已知圓O:ρ=cosθ+sinθ和直線l:![]() .
.
(1)求圓O和直線l的直角坐標方程;
(2)當θ∈(0,π)時,求直線l與圓O公共點的極坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() 兩點在拋物線
兩點在拋物線![]() 上,
上,![]() 是AB的垂直平分線,
是AB的垂直平分線,
(1)當且僅當![]() 取何值時,直線
取何值時,直線![]() 經過拋物線的焦點F?證明你的結論;
經過拋物線的焦點F?證明你的結論;
(2)若![]() ,弦AB是否過定點,若過定點,求出該定點,若不過定點,說明理由.
,弦AB是否過定點,若過定點,求出該定點,若不過定點,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知一個口袋有m個白球,n個黑球(m,n![]()
![]() ,n
,n![]() 2),這些球除顏色外全部相同。現將口袋中的球隨機的逐個取出,并放入如圖所示的編號為1,2,3,……,m+n的抽屜內,其中第k次取球放入編號為k的抽屜(k=1,2,3,……,m+n).
2),這些球除顏色外全部相同。現將口袋中的球隨機的逐個取出,并放入如圖所示的編號為1,2,3,……,m+n的抽屜內,其中第k次取球放入編號為k的抽屜(k=1,2,3,……,m+n).
![]()
(1)試求編號為2的抽屜內放的是黑球的概率p;
(2)隨機變量x表示最后一個取出的黑球所在抽屜編號的倒數,E(x)是x的數學期望,證明 ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著智能手機的發展,各種“APP”(英文單詞Application的縮寫,一般指手機軟件)應運而生.某機構欲對A市居民手機內安裝的APP的個數和用途進行調研,在使用智能手機的居民中隨機抽取100人,獲得了他們手機內安裝APP的個數,整理得到如圖所示頻率分布直方圖.

(Ⅰ)求a的值;
(Ⅱ)從被抽取安裝APP的個數不低于50的居民中,隨機抽取2人進一步調研,求這2人安裝APP的個數都低于60的概率;
(Ⅲ)假設同組中的數據用該組區間的右端點值代替,以本次被抽取的居民情況為參考,試估計A市使用智能手機的居民手機內安裝APP的平均個數在第幾組(只需寫出結論).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】[選修4-4:坐標系與參數方程]
在極坐標系中,O為極點,點![]() 在曲線
在曲線![]() 上,直線l過點
上,直線l過點![]() 且與
且與![]() 垂直,垂足為P.
垂直,垂足為P.
(1)當![]() 時,求
時,求![]() 及l的極坐標方程;
及l的極坐標方程;
(2)當M在C上運動且P在線段OM上時,求P點軌跡的極坐標方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com