
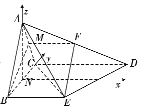
【題目】四棱錐![]() 中,
中, ![]() ,且
,且![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() 是棱
是棱![]() 的中點(diǎn).
的中點(diǎn).

(1)證明: ![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)證明見解析;(2) ![]() .
.
【解析】試題分析:(1)取![]() 中點(diǎn)
中點(diǎn)![]() ,連接
,連接![]() 、
、![]() ,四邊形
,四邊形![]() 是平行四邊形,通過證明
是平行四邊形,通過證明![]() 面ACD,來證明
面ACD,來證明![]() 平面
平面![]() 。(2)取
。(2)取![]() 中點(diǎn)
中點(diǎn)![]() ,過N點(diǎn)做BE的平行線為y軸,NB,NA分別為x,z軸建立空間直角坐標(biāo)系,由空間向量求二面角的余弦值。
,過N點(diǎn)做BE的平行線為y軸,NB,NA分別為x,z軸建立空間直角坐標(biāo)系,由空間向量求二面角的余弦值。
試題解析:(1)取![]() 中點(diǎn)
中點(diǎn)![]() ,連接
,連接![]() 、
、![]() ,
,
∵![]() 是
是![]() 中點(diǎn),∴
中點(diǎn),∴![]() ,且
,且![]() .
.
又因?yàn)?/span>![]() ,∴
,∴![]() .又∵
.又∵![]() ,∴
,∴![]() ,∴四邊形
,∴四邊形![]() 是平行四邊形.∴
是平行四邊形.∴![]() ,又
,又![]() ,∴
,∴![]() 是等邊三角形,∴
是等邊三角形,∴![]() ,∵
,∵![]() 平面
平面![]() ,
, ![]() ,∴
,∴![]() 平面
平面![]() ,∴
,∴![]() ,∴
,∴![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
(2)取![]() 中點(diǎn)
中點(diǎn)![]() ,則
,則![]() ,
, ![]() 平面
平面![]() ,以
,以![]() 為原點(diǎn)建立如圖所示的直角坐標(biāo)系.
為原點(diǎn)建立如圖所示的直角坐標(biāo)系.
各點(diǎn)坐標(biāo)為![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, 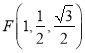 .
.
可得![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
;
設(shè)平面![]() 的法向量
的法向量![]() ,則
,則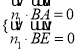 得
得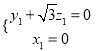 ,
,
取![]() ,
,
設(shè)平面![]() 的法向量
的法向量![]() ,則
,則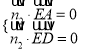 得
得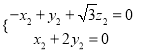 ,
,
取![]() ,
,
于是![]()
![]() ,
,
注意到二面角![]() 是鈍角,因此,所求二面角的余弦值就是
是鈍角,因此,所求二面角的余弦值就是![]() .
.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知拋物線![]() 的準(zhǔn)線與
的準(zhǔn)線與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() ,過點(diǎn)
,過點(diǎn)![]() 作圓
作圓![]() 的兩條切線,切點(diǎn)為
的兩條切線,切點(diǎn)為![]() ,且
,且![]() .
.
(1)求拋物線![]() 的方程;
的方程;
(2)若直線![]() 是過定點(diǎn)
是過定點(diǎn)![]() 的一條直線,且與拋物線
的一條直線,且與拋物線![]() 交于
交于![]() 兩點(diǎn),過定點(diǎn)
兩點(diǎn),過定點(diǎn)![]() 作
作![]() 的垂線與拋物線交于
的垂線與拋物線交于![]() 兩點(diǎn),求四邊形
兩點(diǎn),求四邊形![]() 面積的最小值.
面積的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
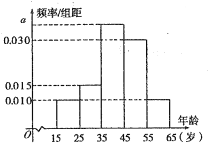
【題目】在某中學(xué)舉行的物理知識競賽中,將三個(gè)年級參賽學(xué)生的成績在進(jìn)行整理后分成5組,繪制出如圖所示的須率分布直方圖,圖中從左到右依次為第一、第二、第三、第四、第五小組.已知第三小組的頻數(shù)是15.

(1)求成績在50-70分的頻率是多少
(2)求這三個(gè)年級參賽學(xué)生的總?cè)藬?shù)是多少:
(3)求成績在80-100分的學(xué)生人數(shù)是多少
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知拋物線![]() 的焦點(diǎn)
的焦點(diǎn)![]() 為曲線
為曲線![]() 的一個(gè)焦點(diǎn),
的一個(gè)焦點(diǎn), ![]() 為坐標(biāo)原點(diǎn),點(diǎn)
為坐標(biāo)原點(diǎn),點(diǎn)![]() 為拋物線
為拋物線![]() 上任意一點(diǎn),過點(diǎn)
上任意一點(diǎn),過點(diǎn)![]() 作
作![]() 軸的平行線交拋物線的準(zhǔn)線于
軸的平行線交拋物線的準(zhǔn)線于![]() ,直線
,直線![]() 交拋物線于點(diǎn)
交拋物線于點(diǎn)![]() .
.
(Ⅰ)求拋物線![]() 的方程;
的方程;
(Ⅱ)若![]() 、
、![]() 、
、![]() 三個(gè)點(diǎn)滿足
三個(gè)點(diǎn)滿足![]() ,求直線
,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,
, ![]()
(Ⅰ)當(dāng)![]() 時(shí),求函數(shù)
時(shí),求函數(shù)![]() 的單調(diào)遞減區(qū)間;
的單調(diào)遞減區(qū)間;
(Ⅱ)若![]() 時(shí),關(guān)于
時(shí),關(guān)于![]() 的不等式
的不等式![]() 恒成立,求實(shí)數(shù)
恒成立,求實(shí)數(shù)![]() 的取值范圍;
的取值范圍;
(Ⅲ)若數(shù)列![]() 滿足
滿足![]() ,
, ![]() ,記
,記![]() 的前
的前![]() 項(xiàng)和為
項(xiàng)和為![]() ,求證:
,求證: ![]() .
.
【答案】(I)![]() ;(II)
;(II)![]() ;(III)證明見解析.
;(III)證明見解析.
【解析】試題分析:(Ⅰ)求出![]() ,在定義域內(nèi),分別令
,在定義域內(nèi),分別令![]() 求得
求得![]() 的范圍,可得函數(shù)
的范圍,可得函數(shù)![]() 增區(qū)間,
增區(qū)間, ![]() 求得
求得![]() 的范圍,可得函數(shù)
的范圍,可得函數(shù)![]() 的減區(qū)間;(Ⅱ)當(dāng)
的減區(qū)間;(Ⅱ)當(dāng)![]() 時(shí),因?yàn)?/span>
時(shí),因?yàn)?/span>![]() ,所以
,所以![]() 顯然不成立,先證明因此
顯然不成立,先證明因此![]() 時(shí),
時(shí), ![]() 在
在![]() 上恒成立,再證明當(dāng)
上恒成立,再證明當(dāng)![]() 時(shí)不滿足題意,從而可得結(jié)果;(III)先求出等差數(shù)列的前
時(shí)不滿足題意,從而可得結(jié)果;(III)先求出等差數(shù)列的前![]() 項(xiàng)和為
項(xiàng)和為![]() ,結(jié)合(II)可得
,結(jié)合(II)可得![]() ,各式相加即可得結(jié)論.
,各式相加即可得結(jié)論.
試題解析:(Ⅰ)由![]() ,得
,得![]() .所以
.所以![]()
令![]() ,解得
,解得![]() 或
或![]() (舍去),所以函數(shù)
(舍去),所以函數(shù)![]() 的單調(diào)遞減區(qū)間為
的單調(diào)遞減區(qū)間為 ![]() .
.
(Ⅱ)由![]() 得,
得, ![]()
當(dāng)![]() 時(shí),因?yàn)?/span>
時(shí),因?yàn)?/span>![]() ,所以
,所以![]() 顯然不成立,因此
顯然不成立,因此![]() .
.
令![]() ,則
,則 ,令
,令![]() ,得
,得![]() .
.
當(dāng)![]() 時(shí),
時(shí), ![]() ,
, ![]() ,∴
,∴![]() ,所以
,所以![]() ,即有
,即有![]() .
.
因此![]() 時(shí),
時(shí), ![]() 在
在![]() 上恒成立.
上恒成立.
②當(dāng)![]() 時(shí),
時(shí), ![]() ,
, ![]() 在
在![]() 上為減函數(shù),在
上為減函數(shù),在![]() 上為增函數(shù),
上為增函數(shù),
∴![]() ,不滿足題意.
,不滿足題意.
綜上,不等式![]() 在
在![]() 上恒成立時(shí),實(shí)數(shù)
上恒成立時(shí),實(shí)數(shù)![]() 的取值范圍是
的取值范圍是![]() .
.
(III)證明:由![]() 知數(shù)列
知數(shù)列![]() 是
是![]() 的等差數(shù)列,所以
的等差數(shù)列,所以![]()
所以![]()
由(Ⅱ)得, ![]() 在
在![]() 上恒成立.
上恒成立.
所以![]() . 將以上各式左右兩邊分別相加,得
. 將以上各式左右兩邊分別相加,得
![]() .因?yàn)?/span>
.因?yàn)?/span>![]()
所以![]()
所以![]() .
.
【題型】解答題
【/span>結(jié)束】
22
【題目】已知直線![]() , (
, (![]() 為參數(shù),
為參數(shù), ![]() 為傾斜角).以坐標(biāo)原點(diǎn)為極點(diǎn),
為傾斜角).以坐標(biāo)原點(diǎn)為極點(diǎn), ![]() 軸的正半軸為極軸建立極坐標(biāo)系,曲線
軸的正半軸為極軸建立極坐標(biāo)系,曲線![]() 的直角坐標(biāo)方程為
的直角坐標(biāo)方程為![]() .
.
(Ⅰ)將曲線![]() 的直角坐標(biāo)方程化為極坐標(biāo)方程;
的直角坐標(biāo)方程化為極坐標(biāo)方程;
(Ⅱ)設(shè)點(diǎn)![]() 的直角坐標(biāo)為
的直角坐標(biāo)為![]() ,直線
,直線![]() 與曲線
與曲線![]() 的交點(diǎn)為
的交點(diǎn)為![]() 、
、![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】樹立和踐行“綠水青山就是金山銀山,堅(jiān)持人與自然和諧共生”的理念越來越深入人心,已形成了全民自覺參與,造福百姓的良性循環(huán).據(jù)此,某網(wǎng)站退出了關(guān)于生態(tài)文明建設(shè)進(jìn)展情況的調(diào)查,調(diào)查數(shù)據(jù)表明,環(huán)境治理和保護(hù)問題仍是百姓最為關(guān)心的熱點(diǎn),參與調(diào)查者中關(guān)注此問題的約占![]() .現(xiàn)從參與關(guān)注生態(tài)文明建設(shè)的人群中隨機(jī)選出200人,并將這200人按年齡分組:第1組
.現(xiàn)從參與關(guān)注生態(tài)文明建設(shè)的人群中隨機(jī)選出200人,并將這200人按年齡分組:第1組![]() ,第2組
,第2組![]() ,第3組
,第3組![]() ,第4組
,第4組![]() ,第5組
,第5組![]() ,得到的頻率分布直方圖如圖所示.
,得到的頻率分布直方圖如圖所示.
(1)求出![]() 的值;
的值;
(2)求這200人年齡的樣本平均數(shù)(同一組數(shù)據(jù)用該區(qū)間的中點(diǎn)值作代表)和中位數(shù)(精確到小數(shù)點(diǎn)后一位);
(3)現(xiàn)在要從年齡較小的第1,2組中用分層抽樣的方法抽取5人,再從這5人中隨機(jī)抽取3人進(jìn)行問卷調(diào)查,求這2組恰好抽到2人的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在四棱錐![]() 中,平面
中,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.

(Ⅰ)求證: ![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)若點(diǎn)![]() 在棱
在棱![]() 上,且
上,且![]() 平面
平面![]() ,求線段
,求線段![]() 的長.
的長.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)的導(dǎo)函數(shù)f '(x)的圖象如圖所示,f(-1)=f(2)=3,令g(x)=(x-1)f(x),則不等式g(x)≥3x-3的解集是( )

A. [-1,1]∪[2,+∞)B. (-∞,-1]∪[1,2]
C. (-∞,-1]∪[2,+∞)D. [-1,2]
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】2020年寒假期間新冠肺炎肆虐,全國人民眾志成城抗疫情.某市要求全體市民在家隔離,同時(shí)決定全市所有學(xué)校推遲開學(xué).某區(qū)教育局為了讓學(xué)生“停課不停學(xué)”,要求學(xué)校各科老師每天在網(wǎng)上授課輔導(dǎo),每天共200分鐘.教育局為了了解高三學(xué)生網(wǎng)上學(xué)習(xí)情況,上課幾天后在全區(qū)高三學(xué)生中采取隨機(jī)抽樣的方法抽取了80名學(xué)生(其中男女生恰好各占一半)進(jìn)行問卷調(diào)查,按男女生分為兩組,再將每組學(xué)生在線學(xué)習(xí)時(shí)間(分鐘)分為5組![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 得到如圖所示的頻率分布直方圖.全區(qū)高三學(xué)生有3000人(男女生人數(shù)大致相等),以頻率估計(jì)概率回答下列問題:
得到如圖所示的頻率分布直方圖.全區(qū)高三學(xué)生有3000人(男女生人數(shù)大致相等),以頻率估計(jì)概率回答下列問題:


(1)估計(jì)全區(qū)高三學(xué)生中網(wǎng)上學(xué)習(xí)時(shí)間不超過40分鐘的人數(shù);
(2)在調(diào)查的80名高三學(xué)生且學(xué)習(xí)時(shí)間不超過40分鐘的學(xué)生中,男女生按分層抽樣的方法抽取6人.若從這6人中隨機(jī)抽取2人進(jìn)行電話訪談,求至少抽到1名男生的概率.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com