
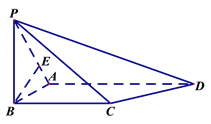
【題目】如圖,在四棱錐![]() 中,平面
中,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.

(Ⅰ)求證: ![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)若點![]() 在棱
在棱![]() 上,且
上,且![]() 平面
平面![]() ,求線段
,求線段![]() 的長.
的長.
【答案】(Ⅰ)見解析. (Ⅱ)![]() .(Ⅲ)
.(Ⅲ)![]() .
.
【解析】試題分析:第一問根據面面垂直的性質和線面垂直的性質得出線線垂直的結論,注意在書寫的時候條件不要丟就行;第二問建立空間直角坐標系,利用法向量所成角的余弦值來求得二面角的余弦值;第三問利用向量共線的關系,得出向量的坐標,根據線面平行得出向量垂直,利用其數量積等于零,求得結果.
(Ⅰ)證明:因為平面![]() ⊥平面
⊥平面![]() ,
,
且平面![]() 平面
平面![]() ,
,
因為![]() ⊥
⊥![]() ,且
,且![]() 平面
平面![]()
所以![]() ⊥平面
⊥平面![]() .
.
因為![]() 平面
平面![]() ,
,
所以![]() ⊥
⊥![]() .
.
(Ⅱ)解:在△![]() 中,因為
中,因為![]() ,
, ![]() ,
, ![]() ,
,
所以![]() ,所以
,所以![]() ⊥
⊥![]() .
.
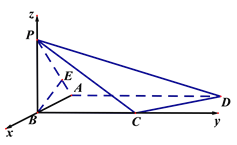
所以,建立空間直角坐標系![]() ,如圖所示.
,如圖所示.
所以![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
易知平面![]() 的一個法向量為
的一個法向量為![]() .
.
設平面![]() 的一個法向量為
的一個法向量為![]() ,
,
則![]() , 即
, 即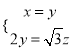 ,
,
令![]() ,則
,則![]() .
.
設二面角![]() 的平面角為
的平面角為![]() ,可知
,可知![]() 為銳角,
為銳角,
則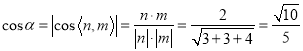 ,
,
即二面角![]() 的余弦值為
的余弦值為![]() .
.
(Ⅲ)解:因為點![]() 在棱
在棱![]() ,所以
,所以![]() ,
, ![]() .
.
因為![]() ,
,
所以![]() ,
, ![]() .
.
又因為![]() 平面
平面![]() ,
, ![]() 為平面
為平面![]() 的一個法向量,
的一個法向量,
所以![]() ,即
,即![]() ,所以
,所以![]() .
.
所以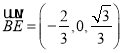 ,所以
,所以![]() .
.


 學而優暑期銜接南京大學出版社系列答案
學而優暑期銜接南京大學出版社系列答案 Happy holiday歡樂假期暑假作業廣東人民出版社系列答案
Happy holiday歡樂假期暑假作業廣東人民出版社系列答案科目:高中數學 來源: 題型:
【題目】如圖所示,甲船由A島出發向北偏東45°的方向作勻速直線航行,速度為![]() nmile/h,在甲船從A島出發的同時,乙船從A島正南
nmile/h,在甲船從A島出發的同時,乙船從A島正南![]() nmile處的B島出發,朝北偏東30°的方向作勻速直線航行,速度為
nmile處的B島出發,朝北偏東30°的方向作勻速直線航行,速度為![]() nmile/h.
nmile/h.

(1)若兩船能相遇,求m;
(2)當![]() 時,兩船出發2小時后,求兩船之間的距離.
時,兩船出發2小時后,求兩船之間的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近年來鄭州空氣污染較為嚴重,現隨機抽取一年(365天)內100天的空氣中![]() 指數的監測數據,統計結果如下:
指數的監測數據,統計結果如下:
|
|
|
|
|
|
|
|
空氣質量 | 優 | 良 | 輕微污染 | 輕度污染 | 中度污染 | 中度重污染 | 重度污染 |
天數 | 4 | 13 | 18 | 30 | 9 | 11 | 15 |
記某企業每天由空氣污染造成的經濟損失為![]() (單位:元),
(單位:元),![]() 指數為
指數為![]() .當
.當![]() 在區間
在區間![]() 內時對企業沒有造成經濟損失;當
內時對企業沒有造成經濟損失;當![]() 在區間
在區間![]() 內時對企業造成經濟損失成直線模型(當
內時對企業造成經濟損失成直線模型(當![]() 指數為150時造成的經濟損失為500元,當
指數為150時造成的經濟損失為500元,當![]() 指數為200時,造成的經濟損失為700元);當
指數為200時,造成的經濟損失為700元);當![]() 指數大于300時造成的經濟損失為2000元.
指數大于300時造成的經濟損失為2000元.
(1)試寫出![]() 的表達式;
的表達式;
(2)試估計在本年內隨機抽取一天,該天經濟損失![]() 大于500元且不超過900元的概率;
大于500元且不超過900元的概率;
(3)若本次抽取的樣本數據有30天是在供暖季,其中有8天為重度污染,完成下面列聯表,并判斷是否有![]() 的把握認為鄭州市本年度空氣重度污染與供暖有關?
的把握認為鄭州市本年度空氣重度污染與供暖有關?
附:
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 1.32 | 2.07 | 2.70 | 3.74 | 5.02 | 6.63 | 7.87 | 10.828 |
![]() ,其中
,其中![]() .
.
非重度污染 | 重度污染 | 合計 | |
供暖季 | |||
非供暖季 | |||
合計 | 100 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近年電子商務蓬勃發展, ![]() 年某網購平臺“雙
年某網購平臺“雙![]() ”一天的銷售業績高達
”一天的銷售業績高達![]() 億元人民幣,平臺對每次成功交易都有針對商品和快遞是否滿意的評價系統.從該評價系統中選出
億元人民幣,平臺對每次成功交易都有針對商品和快遞是否滿意的評價系統.從該評價系統中選出![]() 次成功交易,并對其評價進行統計,網購者對商品的滿意率為
次成功交易,并對其評價進行統計,網購者對商品的滿意率為![]() ,對快遞的滿意率為
,對快遞的滿意率為![]() ,其中對商品和快遞都滿意的交易為
,其中對商品和快遞都滿意的交易為![]() 次.
次.
(1)根據已知條件完成下面的![]() 列聯表,并回答能否有
列聯表,并回答能否有![]() 的把握認為“網購者對商品滿意與對快遞滿意之間有關系”?
的把握認為“網購者對商品滿意與對快遞滿意之間有關系”?
對快遞滿意 | 對快遞不滿意 | 合計 | |
對商品滿意 |
| ||
對商品不滿意 | |||
合計 |
|
(2)為進一步提高購物者的滿意度,平臺按分層抽樣方法從中抽取![]() 次交易進行問卷調查,詳細了解滿意與否的具體原因,并在這
次交易進行問卷調查,詳細了解滿意與否的具體原因,并在這![]() 次交易中再隨機抽取
次交易中再隨機抽取![]() 次進行電話回訪,聽取購物者意見.求電話回訪的
次進行電話回訪,聽取購物者意見.求電話回訪的![]() 次交易至少有一次對商品和快遞都滿意的概率.
次交易至少有一次對商品和快遞都滿意的概率.
附: 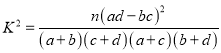 (其中
(其中![]() 為樣本容量)
為樣本容量)
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線![]() 是中心在原點,焦點在
是中心在原點,焦點在![]() 軸上的雙曲線的右支,它的離心率剛好是其對應雙曲線的實軸長,且一條漸近線方程是
軸上的雙曲線的右支,它的離心率剛好是其對應雙曲線的實軸長,且一條漸近線方程是![]() ,線段
,線段![]() 是過曲線
是過曲線![]() 右焦點
右焦點![]() 的一條弦,
的一條弦,![]() 是弦
是弦![]() 的中點。
的中點。
(1)求曲線![]() 的方程;
的方程;
(2)求點![]() 到
到![]() 軸距離的最小值;
軸距離的最小值;
(3)若作出直線![]() ,
,![]() 使點
使點![]() 在直線
在直線![]() 上的射影
上的射影![]() 滿足
滿足![]() .當點
.當點![]() 在曲線
在曲線![]() 上運動時,求
上運動時,求![]() 的取值范圍.
的取值范圍.
(參考公式:若![]() 為雙曲線
為雙曲線![]() 右支上的點,
右支上的點,![]() 為右焦點,則
為右焦點,則![]() .(
.(![]() 為離心率))
為離心率))
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() ,點
,點![]() 與拋物線
與拋物線![]() 的焦點
的焦點![]() 關于原點對稱,過點
關于原點對稱,過點![]() 且斜率為
且斜率為![]() 的直線
的直線![]() 與拋物線
與拋物線![]() 交于不同兩點
交于不同兩點![]() ,線段
,線段![]() 的中點為
的中點為![]() ,直線
,直線![]() 與拋物線
與拋物線![]() 交于兩點
交于兩點![]() .
.
(Ⅰ)判斷是否存在實數![]() 使得四邊形
使得四邊形![]() 為平行四邊形.若存在,求出
為平行四邊形.若存在,求出![]() 的值;若不存在,說明理由;
的值;若不存在,說明理由;
(Ⅱ)求![]() 的取值范圍.
的取值范圍.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com