
【題目】已知函數![]() ,
, ![]()
(Ⅰ)當![]() 時,求函數
時,求函數![]() 的單調遞減區間;
的單調遞減區間;
(Ⅱ)若![]() 時,關于
時,關于![]() 的不等式
的不等式![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍;
的取值范圍;
(Ⅲ)若數列![]() 滿足
滿足![]() ,
, ![]() ,記
,記![]() 的前
的前![]() 項和為
項和為![]() ,求證:
,求證: ![]() .
.
【答案】(I)![]() ;(II)
;(II)![]() ;(III)證明見解析.
;(III)證明見解析.
【解析】試題分析:(Ⅰ)求出![]() ,在定義域內,分別令
,在定義域內,分別令![]() 求得
求得![]() 的范圍,可得函數
的范圍,可得函數![]() 增區間,
增區間, ![]() 求得
求得![]() 的范圍,可得函數
的范圍,可得函數![]() 的減區間;(Ⅱ)當
的減區間;(Ⅱ)當![]() 時,因為
時,因為![]() ,所以
,所以![]() 顯然不成立,先證明因此
顯然不成立,先證明因此![]() 時,
時, ![]() 在
在![]() 上恒成立,再證明當
上恒成立,再證明當![]() 時不滿足題意,從而可得結果;(III)先求出等差數列的前
時不滿足題意,從而可得結果;(III)先求出等差數列的前![]() 項和為
項和為![]() ,結合(II)可得
,結合(II)可得![]() ,各式相加即可得結論.
,各式相加即可得結論.
試題解析:(Ⅰ)由![]() ,得
,得![]() .所以
.所以![]()
令![]() ,解得
,解得![]() 或
或![]() (舍去),所以函數
(舍去),所以函數![]() 的單調遞減區間為
的單調遞減區間為 ![]() .
.
(Ⅱ)由![]() 得,
得, ![]()
當![]() 時,因為
時,因為![]() ,所以
,所以![]() 顯然不成立,因此
顯然不成立,因此![]() .
.
令![]() ,則
,則 ,令
,令![]() ,得
,得![]() .
.
當![]() 時,
時, ![]() ,
, ![]() ,∴
,∴![]() ,所以
,所以![]() ,即有
,即有![]() .
.
因此![]() 時,
時, ![]() 在
在![]() 上恒成立.
上恒成立.
②當![]() 時,
時, ![]() ,
, ![]() 在
在![]() 上為減函數,在
上為減函數,在![]() 上為增函數,
上為增函數,
∴![]() ,不滿足題意.
,不滿足題意.
綜上,不等式![]() 在
在![]() 上恒成立時,實數
上恒成立時,實數![]() 的取值范圍是
的取值范圍是![]() .
.
(III)證明:由![]() 知數列
知數列![]() 是
是![]() 的等差數列,所以
的等差數列,所以![]()
所以![]()
由(Ⅱ)得, ![]() 在
在![]() 上恒成立.
上恒成立.
所以![]() . 將以上各式左右兩邊分別相加,得
. 將以上各式左右兩邊分別相加,得
![]() .因為
.因為![]()
所以![]()
所以![]() .
.
【題型】解答題
【/span>結束】
22
【題目】已知直線![]() , (
, (![]() 為參數,
為參數, ![]() 為傾斜角).以坐標原點為極點,
為傾斜角).以坐標原點為極點, ![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的直角坐標方程為
的直角坐標方程為![]() .
.
(Ⅰ)將曲線![]() 的直角坐標方程化為極坐標方程;
的直角坐標方程化為極坐標方程;
(Ⅱ)設點![]() 的直角坐標為
的直角坐標為![]() ,直線
,直線![]() 與曲線
與曲線![]() 的交點為
的交點為![]() 、
、![]() ,求
,求![]() 的取值范圍.
的取值范圍.
 奪冠訓練單元期末沖刺100分系列答案
奪冠訓練單元期末沖刺100分系列答案 新思維小冠軍100分作業本系列答案
新思維小冠軍100分作業本系列答案 名師指導一卷通系列答案
名師指導一卷通系列答案科目:高中數學 來源: 題型:
【題目】近年來鄭州空氣污染較為嚴重,現隨機抽取一年(365天)內100天的空氣中![]() 指數的監測數據,統計結果如下:
指數的監測數據,統計結果如下:
|
|
|
|
|
|
|
|
空氣質量 | 優 | 良 | 輕微污染 | 輕度污染 | 中度污染 | 中度重污染 | 重度污染 |
天數 | 4 | 13 | 18 | 30 | 9 | 11 | 15 |
記某企業每天由空氣污染造成的經濟損失為![]() (單位:元),
(單位:元),![]() 指數為
指數為![]() .當
.當![]() 在區間
在區間![]() 內時對企業沒有造成經濟損失;當
內時對企業沒有造成經濟損失;當![]() 在區間
在區間![]() 內時對企業造成經濟損失成直線模型(當
內時對企業造成經濟損失成直線模型(當![]() 指數為150時造成的經濟損失為500元,當
指數為150時造成的經濟損失為500元,當![]() 指數為200時,造成的經濟損失為700元);當
指數為200時,造成的經濟損失為700元);當![]() 指數大于300時造成的經濟損失為2000元.
指數大于300時造成的經濟損失為2000元.
(1)試寫出![]() 的表達式;
的表達式;
(2)試估計在本年內隨機抽取一天,該天經濟損失![]() 大于500元且不超過900元的概率;
大于500元且不超過900元的概率;
(3)若本次抽取的樣本數據有30天是在供暖季,其中有8天為重度污染,完成下面列聯表,并判斷是否有![]() 的把握認為鄭州市本年度空氣重度污染與供暖有關?
的把握認為鄭州市本年度空氣重度污染與供暖有關?
附:
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 1.32 | 2.07 | 2.70 | 3.74 | 5.02 | 6.63 | 7.87 | 10.828 |
![]() ,其中
,其中![]() .
.
非重度污染 | 重度污染 | 合計 | |
供暖季 | |||
非供暖季 | |||
合計 | 100 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩家銷售公司擬各招聘一名產品推銷員,日工資方案如下: 甲公司規定底薪80元,每銷售一件產品提成1元; 乙公司規定底薪120元,日銷售量不超過45件沒有提成,超過45件的部分每件提成8元.
(I)請將兩家公司各一名推銷員的日工資![]() (單位: 元) 分別表示為日銷售件數
(單位: 元) 分別表示為日銷售件數![]() 的函數關系式;
的函數關系式;
(II)從兩家公司各隨機選取一名推銷員,對他們過去100天的銷售情況進行統計,得到如下條形圖。若記甲公司該推銷員的日工資為![]() ,乙公司該推銷員的日工資為
,乙公司該推銷員的日工資為![]() (單位: 元),將該頻率視為概率,請回答下面問題:
(單位: 元),將該頻率視為概率,請回答下面問題:
某大學畢業生擬到兩家公司中的一家應聘推銷員工作,如果僅從日均收入的角度考慮,請你利用所學的統計學知識為他作出選擇,并說明理由.
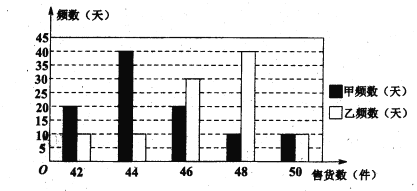
【答案】(I)見解析; (Ⅱ)見解析.
【解析】分析:(I)依題意可得甲公司一名推銷員的工資與銷售件數的關系是一次函數的關系式,而乙公司是分段函數的關系式,由此解得;(Ⅱ)分別根據條形圖求得甲、乙公司一名推銷員的日工資的分布列,從而可分別求得數學期望,進而可得結論.
詳解:(I)由題意得,甲公司一名推銷員的日工資![]() (單位:元) 與銷售件數
(單位:元) 與銷售件數![]() 的關系式為:
的關系式為: ![]() .
.
乙公司一名推銷員的日工資![]() (單位: 元) 與銷售件數
(單位: 元) 與銷售件數![]() 的關系式為:
的關系式為: 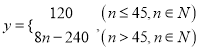
(Ⅱ)記甲公司一名推銷員的日工資為![]() (單位: 元),由條形圖可得
(單位: 元),由條形圖可得![]() 的分布列為
的分布列為
| 122 | 124 | 126 | 128 | 130 |
| 0.2 | 0.4 | 0.2 | 0.1 | 0.1 |
記乙公司一名推銷員的日工資為![]() (單位: 元),由條形圖可得
(單位: 元),由條形圖可得![]() 的分布列為
的分布列為
| 120 | 128 | 144 | 160 |
| 0.2 | 0.3 | 0.4 | 0.1 |
∴![]()
∴僅從日均收入的角度考慮,我會選擇去乙公司.
點睛:求解離散型隨機變量的數學期望的一般步驟為:
第一步是“判斷取值”,即判斷隨機變量的所有可能取值,以及取每個值所表示的意義;
第二步是“探求概率”,即利用排列組合,枚舉法,概率公式,求出隨機變量取每個值時的概率;
第三步是“寫分布列”,即按規范形式寫出分布列,并注意用分布列的性質檢驗所求的分布列或某事件的概率是否正確;
第四步是“求期望值”,一般利用離散型隨機變量的數學期望的定義求期望的值
【題型】解答題
【結束】
19
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 為菱形,
為菱形, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分別是
分別是![]() ,
, ![]() 的中點.
的中點.
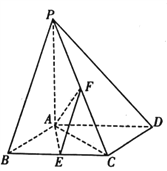
(1)證明: ![]() ;
;
(2)設![]() 為線段
為線段![]() 上的動點,若線段
上的動點,若線段![]() 長的最小值為
長的最小值為![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近年電子商務蓬勃發展, ![]() 年某網購平臺“雙
年某網購平臺“雙![]() ”一天的銷售業績高達
”一天的銷售業績高達![]() 億元人民幣,平臺對每次成功交易都有針對商品和快遞是否滿意的評價系統.從該評價系統中選出
億元人民幣,平臺對每次成功交易都有針對商品和快遞是否滿意的評價系統.從該評價系統中選出![]() 次成功交易,并對其評價進行統計,網購者對商品的滿意率為
次成功交易,并對其評價進行統計,網購者對商品的滿意率為![]() ,對快遞的滿意率為
,對快遞的滿意率為![]() ,其中對商品和快遞都滿意的交易為
,其中對商品和快遞都滿意的交易為![]() 次.
次.
(1)根據已知條件完成下面的![]() 列聯表,并回答能否有
列聯表,并回答能否有![]() 的把握認為“網購者對商品滿意與對快遞滿意之間有關系”?
的把握認為“網購者對商品滿意與對快遞滿意之間有關系”?
對快遞滿意 | 對快遞不滿意 | 合計 | |
對商品滿意 |
| ||
對商品不滿意 | |||
合計 |
|
(2)為進一步提高購物者的滿意度,平臺按分層抽樣方法從中抽取![]() 次交易進行問卷調查,詳細了解滿意與否的具體原因,并在這
次交易進行問卷調查,詳細了解滿意與否的具體原因,并在這![]() 次交易中再隨機抽取
次交易中再隨機抽取![]() 次進行電話回訪,聽取購物者意見.求電話回訪的
次進行電話回訪,聽取購物者意見.求電話回訪的![]() 次交易至少有一次對商品和快遞都滿意的概率.
次交易至少有一次對商品和快遞都滿意的概率.
附: 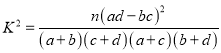 (其中
(其中![]() 為樣本容量)
為樣本容量)
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線![]() 是中心在原點,焦點在
是中心在原點,焦點在![]() 軸上的雙曲線的右支,它的離心率剛好是其對應雙曲線的實軸長,且一條漸近線方程是
軸上的雙曲線的右支,它的離心率剛好是其對應雙曲線的實軸長,且一條漸近線方程是![]() ,線段
,線段![]() 是過曲線
是過曲線![]() 右焦點
右焦點![]() 的一條弦,
的一條弦,![]() 是弦
是弦![]() 的中點。
的中點。
(1)求曲線![]() 的方程;
的方程;
(2)求點![]() 到
到![]() 軸距離的最小值;
軸距離的最小值;
(3)若作出直線![]() ,
,![]() 使點
使點![]() 在直線
在直線![]() 上的射影
上的射影![]() 滿足
滿足![]() .當點
.當點![]() 在曲線
在曲線![]() 上運動時,求
上運動時,求![]() 的取值范圍.
的取值范圍.
(參考公式:若![]() 為雙曲線
為雙曲線![]() 右支上的點,
右支上的點,![]() 為右焦點,則
為右焦點,則![]() .(
.(![]() 為離心率))
為離心率))
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】數列![]() 中,
中,![]() 在直線
在直線![]() .
.
(1)求數列{an}的通項公式;
(2)令![]() ,數列
,數列![]() 的前n項和為
的前n項和為![]() .
.
(ⅰ)求![]() ;
;
(ⅱ)是否存在整數λ![]() ,使得不等式(-1)nλ<
,使得不等式(-1)nλ<![]() (n∈N
(n∈N![]() )恒成立?若存在,求出λ的取值的集合;若不存在,請說明理由.
)恒成立?若存在,求出λ的取值的集合;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com