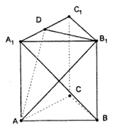
如圖,直三棱柱
ABC-
A1B1C1中,底面是等腰直角三角形,
AB=
BC=
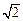
,
BB1=3,
D為
A1C1的中點(diǎn),
F在線段
AA1上.
(1)
AF為何值時,
CF⊥平面
B1DF?
(2)設(shè)
AF=1,求平面
B1CF與平面
ABC所成的銳二面角的余弦值.

(1)
AF=1或2時,
CF⊥平面
B1DF(2)銳二面角的余弦值

(1)因?yàn)橹比庵?i>ABC-
A1B1C1中,
 BB1
BB1⊥面
ABC,∠
ABC=

.
以
B點(diǎn)為原點(diǎn),
BA、
BC、
BB1分別為
x、
y、
z軸建立如圖所示空間直角坐標(biāo)系.
因?yàn)?i>AC=2,∠
ABC=90º,所以
AB=
BC=,
從而
B(0,0,0),
A
,
C
,
B1(0,0,3),
A1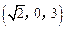
,
C1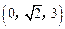
,
D
,
E
.
所以

,
設(shè)
AF=
x,則
F(,0,
x),

.

,所以

要使
CF⊥平面
B1DF,只需
CF⊥
B1F.
由

=2+
x(
x-3)=0,得
x=1或
x=2,
故當(dāng)
AF=1或2時,
CF⊥平面
B1DF.……………… 5分
(2)由(1)知平面
ABC的法向量為
n1=(0,0,1).
設(shè)平面
B1CF的法向量為
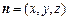
,則由

得

令
z=1得

,
所以平面
B1CF與平面
ABC所成的銳二面角的余弦值

………………… 10分
練習(xí)冊系列答案
相關(guān)習(xí)題
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
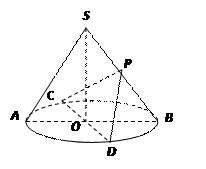
如圖,圓錐
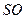
中,
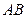
、
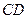
為底面圓的兩條直徑,
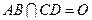
,且
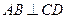
,
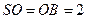
,
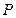
為
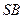
的中點(diǎn).
(1)求圓錐
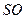
的表面積;
(2)求異面直線
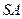
與
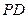
所成角的正切值.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
已知直角梯形ABCD中,AD∥BC,AB⊥AD,∠C=45°,AD=AB=2,把梯形沿BD折起成60°的二面角C′-BD-A.求: (1)C′到平面ADB的距離;
(2)AC′與BD所成的角.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
如圖,在四棱錐
P—ABCD中,
PD⊥底面
ABCD,底面
ABCD為正方形,
PD=
DC,
E、
F分別是
AB,
PB的中點(diǎn).

(I)求證:
EF⊥
CD;
(II)求
DB與平面
DEF所成角的正弦值;
(III)在平面
PAD內(nèi)是否存在一點(diǎn)
G,使
G在平面
PCB上的射影為△
PCB的外心,若存在,試確定點(diǎn)
G的位置;若不存在,說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
右圖幾何體是由下邊的哪一個平面圖形旋轉(zhuǎn)而形成的( )
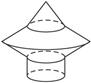
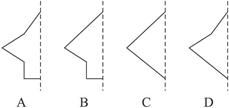
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
正方體ABCD-A1B1C1D1中,P為面A1B1C1D1的中心,求證:PA⊥PB1.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
(1)求證:
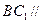
平面
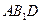
(2)求二面角
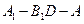
的大小
(3)求直線AB與平面
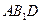
所成線面角的正弦值
查看答案和解析>>

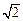 ,BB1=3,D為A1C1的中點(diǎn),F在線段AA1上.
,BB1=3,D為A1C1的中點(diǎn),F在線段AA1上.


 .
. ,C
,C ,B1(0,0,3),A1
,B1(0,0,3),A1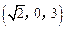 ,C1
,C1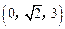 ,D
,D ,E
,E .
. ,
, .
. ,所以
,所以
 =2+x(x-3)=0,得x=1或x=2,
=2+x(x-3)=0,得x=1或x=2,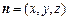 ,則由
,則由 得
得
 ,
,


 快捷英語周周練系列答案
快捷英語周周練系列答案
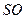 中,
中,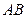 、
、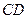 為底面圓的兩條直徑,
為底面圓的兩條直徑,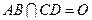 ,且
,且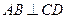 ,
,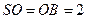 ,
,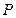 為
為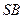 的中點(diǎn).
的中點(diǎn).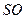 的表面積;
的表面積; 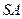 與
與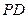 所成角的正切值.
所成角的正切值.
