
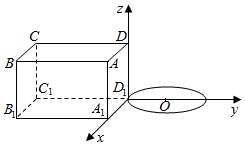
 如圖所示,在長方體ABCD-A1B1C1D1中,AB=BC=2,DD1=1.
如圖所示,在長方體ABCD-A1B1C1D1中,AB=BC=2,DD1=1.分析 (1)證明B1D1⊥A1C1,B1D1⊥CC1,即可證明B1D1⊥平面C1A1AC;
(2)(I)由題意sin∠OC1P=$\frac{1}{3}$,即可求C1N長度;
(Ⅱ)由(I)可知C1P=2$\sqrt{2}$,sin2∠OC1P=2×$\frac{1}{3}×\frac{2\sqrt{2}}{3}$=$\frac{4\sqrt{2}}{9}$,即可求$\overrightarrow{CQ}$•$\overrightarrow{CP}$的取值范圍.
解答 (1)證明:在長方體ABCD-A1B1C1D1中,AB=BC,
∴B1D1⊥A1C1,B1D1⊥CC1,
∵A1C1∩CC1=C1,
∴B1D1⊥平面C1A1AC;
(2)(I)解:由題意sin∠OC1P=$\frac{1}{3}$,
∴cos∠OC1P=$\frac{2\sqrt{2}}{3}$,
∴C1N=$\frac{2}{\frac{2\sqrt{2}}{3}}$=$\frac{3}{2}\sqrt{2}$;
(Ⅱ)由(I)可知C1P=2$\sqrt{2}$,sin2∠OC1P=2×$\frac{1}{3}×\frac{2\sqrt{2}}{3}$=$\frac{4\sqrt{2}}{9}$,
∴cos2∠OC1P=$\frac{7}{9}$,
∴$\overrightarrow{CQ}$•$\overrightarrow{CP}$的最小值為$\frac{56}{9}$,最大值為8,
∴$\overrightarrow{CQ}$•$\overrightarrow{CP}$的取值范圍是[$\frac{56}{9}$,8].
點評 本題考查線面垂直,考查平面向量知識的運用,考查學生分析解決問題的能力,屬于中檔題.


科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
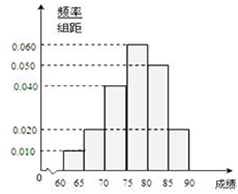 在某次綜合素質測試中,共設有40個考室,每個考室30名考生.在考試結束后,為調查其測試前的培訓輔導情況與測試成績的相關性,抽取每個考室中座位號為05的考生,得到40名考生,統計他們的成績,得到如圖所示的頻率分布直方圖:
在某次綜合素質測試中,共設有40個考室,每個考室30名考生.在考試結束后,為調查其測試前的培訓輔導情況與測試成績的相關性,抽取每個考室中座位號為05的考生,得到40名考生,統計他們的成績,得到如圖所示的頻率分布直方圖:查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 如圖,在底面為菱形的四棱錐P-ABCD中,PA⊥平面ABCD,E為PD的中點,AB=2,∠ABC=$\frac{π}{3}$.
如圖,在底面為菱形的四棱錐P-ABCD中,PA⊥平面ABCD,E為PD的中點,AB=2,∠ABC=$\frac{π}{3}$.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com