
分析 (Ⅰ)設數列{an}的公差為d,由題意、等比中項的性質、等差數列的通項公式列出方程組,求出a1和d,代入等差數列的通項公式求出an;
(Ⅱ)由(Ⅰ)化簡bn=$\frac{1}{{a}_{n+1}{a}_{n+3}}$,利用裂項相消法數列{bn}的前n項和Tn.
解答 解:(Ⅰ)設數列{an}的公差為d,
∵a2,a3,a5成等比數列,a1+a2=1,
∴$\left\{\begin{array}{l}{{({a}_{1}+2d)}^{2}=({a}_{1}+d)({a}_{1}+4d)}\\{2{a}_{1}+d=1}\end{array}\right.$,
又d≠0,解得d=1,a1=0,
∴an=a1+(n-1)d=n-1;
(Ⅱ)由(I)得an=n-1,則bn=$\frac{1}{{a}_{n+1}{a}_{n+3}}$=$\frac{1}{n(n+2)}$
=$\frac{1}{2}$($\frac{1}{n}-\frac{1}{n+2}$),
∴Tn=$\frac{1}{2}$[(1-$\frac{1}{3}$)+($\frac{1}{2}-\frac{1}{4}$)+($\frac{1}{3}-\frac{1}{5}$)+…+($\frac{1}{n-1}-\frac{1}{n+1}$)+($\frac{1}{n}-\frac{1}{n+2}$)]
=$\frac{1}{2}(1+\frac{1}{2}-\frac{1}{n+1}-\frac{1}{n+2})$=$\frac{3{n}^{2}+5n}{4(n+1)(n+2)}$,
∴數列{bn}的前n項和Tn=$\frac{3{n}^{2}+5n}{4(n+1)(n+2)}$.
點評 本題考查等差數列的通項公式,等比中項的性質,以及裂項相消法求數列的和,考查方程思想,化簡、變形能力.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
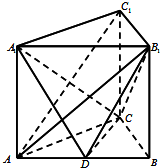 如圖,三棱柱ABC-A1B1C1側棱垂直于底面,AB=4,AC=BC=3,D為AB的中點.
如圖,三棱柱ABC-A1B1C1側棱垂直于底面,AB=4,AC=BC=3,D為AB的中點.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{2}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | 2 | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | -1 | C. | -$\frac{3}{4}$ | D. | -2 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com