
分析 (1)利用導數直接確定單調區間;
(2))①只需x2-2x+a>0在(-∞,1)∪(1,+∞)恒成立即可;
②不等式f(x)<(x-1)•ex對任意的x∈(1,+∞)都成立?ln(x2-2x+a)<(x-1)2ex對任意的x∈(1,+∞)都成立.
令g(x)=ln(x2-2x+a)-(x-1)2ex,x∈(1,+∞),只要g(x)max<0 即可.
解答 解:(1)當當a=1,x∈(1,+∞)時,f(x)=$\frac{ln({x}^{2}-2x+a)}{x-1}$=$\frac{2ln(x-1)}{x-1}$.
f′(x)=$\frac{2-2ln(x-1)}{x-1}$=0⇒x=e+1,
x∈(1,e+1)時,f′(x)>0,x∈(e+1,+∞),f′(x)<0,
函數f(x)在(e+1,+∞)上的單調遞減,在∈(1,e+1)遞增.
(2)①∵f(x)的定義域為(-∞,1)∪(1,+∞),∴x2-2x+a>0在(-∞,1)∪(1,+∞)恒成立,∴a≥1;
②不等式f(x)<(x-1)•ex對任意的x∈(1,+∞)都成立?ln(x2-2x+a)<(x-1)2ex對任意的x∈(1,+∞)都成立.
令g(x)=ln(x2-2x+a)-(x-1)2ex,x∈(1,+∞).$g′(x)=\frac{2x-2}{{x}^{2}-2x+a}-{e}^{x}({x}^{2}-1)$=(x-1)[$\frac{2}{{x}^{2}-2x+a}-(x+1){e}^{x}$]
令h(x)=$\frac{2}{{x}^{2}-2x+a}-(x+1){e}^{x}$∵$y=\frac{2}{{x}^{2}-2x+a}在(1,+∞)遞增,y=(x+1)^{2}{e}^{x}$在(1,+∞)遞減,
∴h(x)在(1,+∞)遞減,∴$h(x)<h(1)=\frac{2}{a-1}-2e$.
當h(1)=$\frac{2}{a-1}-2e≤0$時,即a$≥1+\frac{1}{e}$時,g′(x)<0,∴g(x)在(1,+∞)遞減,
∴g(x)<g(1)=ln(a-1)≤0即可⇒a≤2,綜上:1+$\frac{1}{e}$≤a≤2符合題意.
當h(1)>0時,即1≤a<1+$\frac{1}{e}$時,存在x0>1,使h(x0)=$\frac{2}{{{x}_{0}}^{2}-2x+a}-({x}_{0}+1){e}^{{x}_{0}}=0$,
x∈(1,x0)時,h(x)>0,x∈(x0,+∞)時,h(x)<0,
g(x)在(1,x0)遞增,在(x0,+∞)遞減,∴g(x)max=g(x0)=ln(x02-2x0+a)-(x0-1)2ex0=ln$\frac{2}{{e}^{{x}_{0}}({x}_{0}+1)}-({x}_{0}-1)^{2}{e}^{{x}_{0}}<0$恒成立,即1≤a<1+$\frac{1}{e}$符合題意.
所以綜上:關于x的不等式f(x)<(x-1)•ex對任意的x∈(1,+∞)都成立,實數a的取值范圍:[1,2]
點評 本題考查了利用導數處理函數單調性的基本方法,及構造新函數處理函數不等式恒成立問題的基本技巧,屬于難題.


 唐印文化課時測評系列答案
唐印文化課時測評系列答案 導學與測試系列答案
導學與測試系列答案科目:高中數學 來源: 題型:解答題
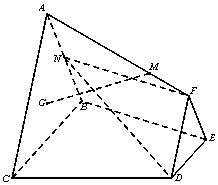 如圖,已知平面ABC⊥平面BCDE,△DEF與△ABC分別是棱長為1與2的正三角形,AC∥DF,四邊形BCDE為直角梯形,DE∥BC,BC⊥CD,CD=1,點G為△ABC的重心,N為AB中點,$\overrightarrow{AM}$=λ$\overrightarrow{AF}$(λ∈r,λ>0),
如圖,已知平面ABC⊥平面BCDE,△DEF與△ABC分別是棱長為1與2的正三角形,AC∥DF,四邊形BCDE為直角梯形,DE∥BC,BC⊥CD,CD=1,點G為△ABC的重心,N為AB中點,$\overrightarrow{AM}$=λ$\overrightarrow{AF}$(λ∈r,λ>0),查看答案和解析>>
科目:高中數學 來源: 題型:填空題
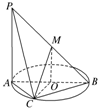 如圖,AB為圓O的直徑,點C在圓周上(異于點A,B),直線PA垂直于圓O所在的平面,點M是線段PB的中點.有以下四個命題:
如圖,AB為圓O的直徑,點C在圓周上(異于點A,B),直線PA垂直于圓O所在的平面,點M是線段PB的中點.有以下四個命題:查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 向左平移$\frac{3π}{4}$個單位長度 | B. | 向右平移$\frac{3π}{4}$個單位長度 | ||
| C. | 向左平移$\frac{3π}{16}$個單位長度 | D. | 向右平移$\frac{3π}{16}$個單位長度 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 2 | B. | 3 | C. | 1+lg99 | D. | 2+lg99 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -$\frac{1}{9}$ | B. | -$\frac{2}{9}$ | C. | -$\frac{1}{3}$ | D. | -$\frac{7}{18}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com