
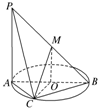
 如圖,AB為圓O的直徑,點C在圓周上(異于點A,B),直線PA垂直于圓O所在的平面,點M是線段PB的中點.有以下四個命題:
如圖,AB為圓O的直徑,點C在圓周上(異于點A,B),直線PA垂直于圓O所在的平面,點M是線段PB的中點.有以下四個命題:分析 ①先證明MO∥PA,即可判定MO∥平面PAC;
②PA在平面MOB內,可得①錯誤;
③可證PA⊥BC,BC⊥平面PAC.即可證明OC⊥平面PAC不成立;
④由③知BC⊥平面PAC,即可證明平面PAC⊥平面PBC.
解答  解:①因為MO∥PA,MO?平面PAC,PA?平面PAC,所以MO∥平面PAC;
解:①因為MO∥PA,MO?平面PAC,PA?平面PAC,所以MO∥平面PAC;
②因為PA在平面MOB內,所以①錯誤;
③因為PA垂直于圓O所在的平面,所以PA⊥BC.
又BC⊥AC,AC∩PA=A,所以BC⊥平面PAC.因為空間內過一點作已知平面的垂線有且只有一條,所以OC⊥平面PAC不成立,③錯誤;
④由③知BC⊥平面PAC,且BC?平面PBC,所以平面PAC⊥平面PBC.
正確命題的序號是①④.
故答案為:①④.
點評 本題主要考查了直線與平面平行的判定,直線與平面垂直的性質,考查了空間想象能力和推理論證能力,考查了數(shù)形結合思想的應用,屬于中檔題.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數(shù)學 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:選擇題
| A. | 2n+1 | B. | 2n-3 | C. | 2n-1 | D. | 2n |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:選擇題
| A. | [-$\sqrt{3}$,$\sqrt{3}$] | B. | (-$\sqrt{3}$,$\sqrt{3}$) | C. | (-∞,-$\sqrt{3}$)∪($\sqrt{3}$,+∞) | D. | (-∞,-$\sqrt{3}$]∪[$\sqrt{3}$,+∞) |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com