
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\sqrt{2}$ | C. | $\frac{\sqrt{2}}{2}$+1 | D. | 2 |
分析 利用點到直線的距離公式求出圓心到直線的距離d,由d-r求出最小值,最大值為(0,2)到直線的距離,確定出a與b的值,即可求出a-b的值.
解答 解:將x=$\sqrt{2y-{y}^{2}}$化為:x2+(y-1)2=1,
∴圓心(0,1),半徑r=1,
∵圓心到直線x-y-2=0的距離d=$\frac{3\sqrt{2}}{2}$,
∴圓上的點到直線的最小距離b=$\frac{3\sqrt{2}}{2}$-1,
最大值為(0,2)到直線的距離,即a=$\frac{4}{\sqrt{2}}$=2$\sqrt{2}$
則a-b=$\frac{\sqrt{2}}{2}$+1.
故選C.
點評 此題考查了直線與圓的位置關系,涉及的知識有:圓的標準方程,點到直線的距離公式,屬于中檔題.


 學練快車道快樂假期寒假作業系列答案
學練快車道快樂假期寒假作業系列答案 新思維寒假作業系列答案
新思維寒假作業系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
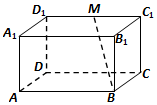 如圖,在長方體ABCD-A1B1C1D1中,AB=2AD=4,A A1=2$\sqrt{2}$,M是C1D1的中點.
如圖,在長方體ABCD-A1B1C1D1中,AB=2AD=4,A A1=2$\sqrt{2}$,M是C1D1的中點.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | p2 | B. | p2(1-p) | C. | ${C}_{3}^{2}$p2 | D. | ${C}_{3}^{2}$p2(1-p) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 2016年1月1日,我國實施“全面二孩”政策,中國社會科學院在某地隨機抽取了150名已婚男性,其中愿意生育二孩的有100名,經統計,該100名男性的年齡情況對應的頻率分布直方圖如下:
2016年1月1日,我國實施“全面二孩”政策,中國社會科學院在某地隨機抽取了150名已婚男性,其中愿意生育二孩的有100名,經統計,該100名男性的年齡情況對應的頻率分布直方圖如下:查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ | B. | $\frac{x^2}{4}+{y^2}=1$ | C. | ${x^2}+\frac{y^2}{4}=1$ | D. | $\frac{{x}^{2}}{2}$+$\frac{y^2}{4}$=1 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | [0,$\frac{2}{3}$) | B. | [0,$\frac{3}{4}$) | C. | ($\frac{3}{4}$,+∞) | D. | (0,$\frac{2}{3}$) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com