
【題目】已知函數(shù)![]() .
.
(1)求![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)若![]() 在
在![]() 上的最大值是
上的最大值是![]() ,求
,求![]() 的值;
的值;
(3)記![]() ,當(dāng)
,當(dāng)![]() 時(shí),若對(duì)任意
時(shí),若對(duì)任意![]() ,總有
,總有![]() 成立,試求
成立,試求![]() 的最大值.
的最大值.
【答案】(1)增區(qū)間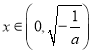 ;減區(qū)間
;減區(qū)間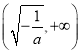 ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
試題分析:(1)借助題設(shè)條件運(yùn)用導(dǎo)數(shù)的知識(shí)求解;(2)借助題設(shè)運(yùn)用分類整合思想探求;(3)借助題設(shè)構(gòu)造函數(shù),運(yùn)用導(dǎo)數(shù)的有關(guān)知識(shí)分析探求.
試題解析:
(1)![]() 的定義域是
的定義域是![]() .
.![]() .當(dāng)
.當(dāng)![]() 時(shí),
時(shí),![]() ,故
,故![]() 在
在![]() 上是增函數(shù); 當(dāng)
上是增函數(shù); 當(dāng)![]() 時(shí),令
時(shí),令![]() ,則
,則![]() (舍去); 當(dāng)
(舍去); 當(dāng)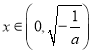 時(shí),
時(shí),![]() ,故
,故![]() 在
在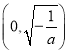 上是增函數(shù);當(dāng)
上是增函數(shù);當(dāng)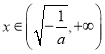 時(shí),
時(shí),![]() ,故
,故![]() 在
在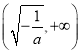 上是減函數(shù).
上是減函數(shù).
(2)①當(dāng)![]() 時(shí),
時(shí),![]() 在
在![]() 上是增函數(shù); 故在
上是增函數(shù); 故在![]() 上的最大值是
上的最大值是 ![]() ,顯然不合題意. ②若
,顯然不合題意. ②若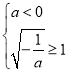 , 即
, 即![]() 時(shí),
時(shí), 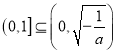 ,則
,則![]() 在
在![]() 上是增函數(shù),故在
上是增函數(shù),故在![]() 上的最大值是
上的最大值是 ![]() ,不合題意,舍去.
,不合題意,舍去.
③ 若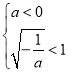 , 即
, 即![]() 時(shí),
時(shí),![]() 在
在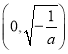 上是增函數(shù) ,在
上是增函數(shù) ,在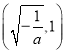 上是減函數(shù),故在
上是減函數(shù),故在![]() 上的最大值是
上的最大值是 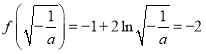 , 解得
, 解得![]() ,符合. 綜合①、②、③得:
,符合. 綜合①、②、③得: ![]() .
.
(3)![]() , 則
, 則![]() ,當(dāng)
,當(dāng)![]() 時(shí),
時(shí),![]() ,故
,故![]() 時(shí),當(dāng)
時(shí),當(dāng)![]() 在
在![]() 上是減函數(shù),不妨設(shè)
上是減函數(shù),不妨設(shè)![]() ,則
,則![]() ,故
,故![]() 等價(jià)于
等價(jià)于![]() ,即
,即![]() ,記
,記
![]() ,從而
,從而![]() 在
在![]() 上為減函數(shù),由
上為減函數(shù),由![]() 得:
得:
![]() ,故
,故![]() 恒成立,
恒成立,![]() ,又
,又
![]() 在
在![]() 上單調(diào)遞減,
上單調(diào)遞減,
![]() ,
,![]() .故當(dāng)
.故當(dāng)![]() 時(shí),
時(shí),![]() 的最大值為
的最大值為![]() .
.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)樣本x1,x2,…,x10數(shù)據(jù)的平均值和方差分別為3和5,若yi=xi+a(a為非零實(shí)數(shù),i=1,2,…,10),則y1,y2,…,y10的均值和方差分別為( )
A. 3,5 B. 3+a,5 C. 3+a,5+a D. 3,5+a
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知![]() ,設(shè)函數(shù)
,設(shè)函數(shù)![]() .
.
(1)存在![]() ,使得
,使得![]() 是
是![]() 在
在![]() 上的最大值,求
上的最大值,求![]() 的取值范圍;
的取值范圍;
(2)![]() 對(duì)任意
對(duì)任意![]() 恒成立時(shí),
恒成立時(shí),![]() 的最大值為1,求
的最大值為1,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】為了傳承經(jīng)典,促進(jìn)學(xué)生課外閱讀,某校從高中年級(jí)和初中年級(jí)各隨機(jī)抽取100名學(xué)生進(jìn)行有關(guān)對(duì)中國(guó)四大名著常識(shí)了解的競(jìng)賽.圖1和圖2分別是高中年級(jí)和初中年級(jí)參加競(jìng)賽的學(xué)生成績(jī)按照![]() 分組,得到的頻率分布直方圖.
分組,得到的頻率分布直方圖.
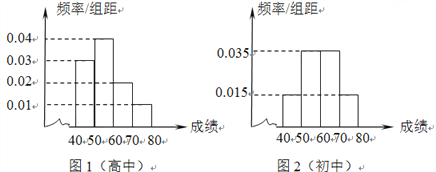
(1)分別計(jì)算參加這次知識(shí)競(jìng)賽的兩個(gè)學(xué)段的學(xué)生的平均成績(jī);
(2)規(guī)定競(jìng)賽成績(jī)達(dá)到![]() 為優(yōu)秀,經(jīng)統(tǒng)計(jì)初中年級(jí)有3名男同學(xué),2名女同學(xué)達(dá)到優(yōu)秀,現(xiàn)從上述5人中任選兩人參加復(fù)試,求選中的2人恰好都為女生的概率;
為優(yōu)秀,經(jīng)統(tǒng)計(jì)初中年級(jí)有3名男同學(xué),2名女同學(xué)達(dá)到優(yōu)秀,現(xiàn)從上述5人中任選兩人參加復(fù)試,求選中的2人恰好都為女生的概率;
(3)完成下列![]() 的列聯(lián)表,并回答是否有99%的把握認(rèn)為“兩個(gè)學(xué)段的學(xué)生對(duì)四大名著的了解有差異”?
的列聯(lián)表,并回答是否有99%的把握認(rèn)為“兩個(gè)學(xué)段的學(xué)生對(duì)四大名著的了解有差異”?
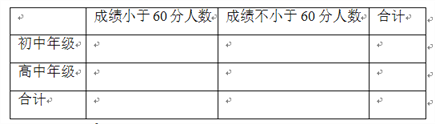
附: 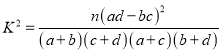
臨界值表:
| 0.10 | 0.05 | 0.01 |
| 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若存在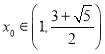 ,使函數(shù)
,使函數(shù)![]() 的圖像在點(diǎn)
的圖像在點(diǎn)![]() 和點(diǎn)
和點(diǎn)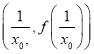 處的切線互相垂直,求
處的切線互相垂直,求![]() 的取值范圍;
的取值范圍;
(3)若函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上有兩個(gè)極值點(diǎn),則是否存在實(shí)數(shù)
上有兩個(gè)極值點(diǎn),則是否存在實(shí)數(shù)![]() ,使
,使![]() 對(duì)任意的
對(duì)任意的![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的取值范圍,若不存在,說(shuō)明理由.
的取值范圍,若不存在,說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某工廠第一季度某產(chǎn)品月生產(chǎn)量依次為10萬(wàn)件,12萬(wàn)件,13萬(wàn)件,為了預(yù)測(cè)以后每個(gè)月的產(chǎn)量,以這3個(gè)月的產(chǎn)量為依據(jù),用一個(gè)函數(shù)模擬該產(chǎn)品的月產(chǎn)量![]() (單位:萬(wàn)件)與月份
(單位:萬(wàn)件)與月份![]() 的關(guān)系. 模擬函數(shù)
的關(guān)系. 模擬函數(shù)![]() ;模擬函數(shù)
;模擬函數(shù)![]() .
.
(1)已知4月份的產(chǎn)量為萬(wàn)件,問選用哪個(gè)函數(shù)作為模擬函數(shù)好?
(2)受工廠設(shè)備的影響,全年的每月產(chǎn)量都不超過(guò)15萬(wàn)件,請(qǐng)選用合適的模擬函數(shù)預(yù)測(cè)6月份的產(chǎn)量.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知![]() 為拋物線
為拋物線![]() :
: ![]() (
(![]() )的焦點(diǎn),直線
)的焦點(diǎn),直線![]() :
: ![]() 交拋物線
交拋物線![]() 于
于![]() ,
, ![]() 兩點(diǎn).
兩點(diǎn).
(Ⅰ)當(dāng)![]() ,
, ![]() 時(shí),求拋物線
時(shí),求拋物線![]() 的方程;
的方程;
(Ⅱ)過(guò)點(diǎn)![]() ,
, ![]() 作拋物線
作拋物線![]() 的切線,
的切線, ![]() ,
, ![]() 交點(diǎn)為
交點(diǎn)為![]() ,若直線
,若直線![]() 與直線
與直線![]() 斜率之和為
斜率之和為![]() ,求直線
,求直線![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某種產(chǎn)品的年銷售量![]() 與該年廣告費(fèi)用支出
與該年廣告費(fèi)用支出![]() 有關(guān),現(xiàn)收集了4組觀測(cè)數(shù)據(jù)列于下表:
有關(guān),現(xiàn)收集了4組觀測(cè)數(shù)據(jù)列于下表:
| 1 | 4 | 5 | 6 |
| 30 | 40 | 60 | 50 |
現(xiàn)確定以廣告費(fèi)用支出![]() 為解釋變量,銷售量
為解釋變量,銷售量![]() 為預(yù)報(bào)變量對(duì)這兩個(gè)變量進(jìn)行統(tǒng)計(jì)分析.
為預(yù)報(bào)變量對(duì)這兩個(gè)變量進(jìn)行統(tǒng)計(jì)分析.
(1)已知這兩個(gè)變量滿足線性相關(guān)關(guān)系,試建立![]() 與
與![]() 之間的回歸方程;
之間的回歸方程;
(2)假如2017年廣告費(fèi)用支出為10萬(wàn)元,請(qǐng)根據(jù)你得到的模型,預(yù)測(cè)該年的銷售量![]() .
.
(線性回歸方程系數(shù)公式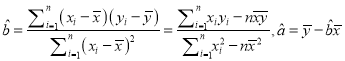 ).
).
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某高校大一新生中的6名同學(xué)打算參加學(xué)校組織的“雅荷文學(xué)社”、“青春風(fēng)街舞社”、“羽乒協(xié)會(huì)”、“演講團(tuán)”、“吉他協(xié)會(huì)”五個(gè)社團(tuán),若每名同學(xué)必須參加且只能參加1個(gè)社團(tuán)且每個(gè)社團(tuán)至多兩人參加,則這6個(gè)人中至多有1人參加“演講團(tuán)”的不同參加方法數(shù)為( )
A. 4680 B. 4770 C. 5040 D. 5200
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com