
【題目】已知![]() ,設(shè)函數(shù)
,設(shè)函數(shù)![]() .
.
(1)存在![]() ,使得
,使得![]() 是
是![]() 在
在![]() 上的最大值,求
上的最大值,求![]() 的取值范圍;
的取值范圍;
(2)![]() 對任意
對任意![]() 恒成立時,
恒成立時,![]() 的最大值為1,求
的最大值為1,求![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ;(2)
;(2) ![]() .
.
【解析】
試題分析:(1)求函數(shù)![]() 的導(dǎo)數(shù)得
的導(dǎo)數(shù)得![]() ,分別討論
,分別討論![]() 時函數(shù)
時函數(shù)![]() 在區(qū)間
在區(qū)間![]() 的最大值點是否符合題意即可;
的最大值點是否符合題意即可;
(2)![]() ,構(gòu)造函數(shù)
,構(gòu)造函數(shù)![]() ,道
,道![]() 的最大值為
的最大值為![]() ,等價于
,等價于![]() 在區(qū)間
在區(qū)間![]() 上恒成立,由于
上恒成立,由于![]() ,則
,則![]() ,此時
,此時![]() 恒成立,即
恒成立,即![]() 在區(qū)間
在區(qū)間![]() 上單調(diào)遞增,符合題意.
上單調(diào)遞增,符合題意.
試題解析:(1)![]() ,
,
①當![]() 時,
時,![]() 在
在![]() 上單調(diào)遞增,在
上單調(diào)遞增,在![]() 單調(diào)遞減,在
單調(diào)遞減,在![]() 單調(diào)遞增,
單調(diào)遞增,
∴![]() ,由
,由![]() ,得
,得![]() 在
在![]() 時無解,
時無解,
②當![]() 時,不合題意;
時,不合題意;
③當![]() 時,
時,![]() 在
在![]() 單調(diào)遞增,在
單調(diào)遞增,在![]() 遞減,在
遞減,在![]() 單調(diào)遞增,
單調(diào)遞增,
∴![]() 即
即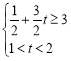 ,∴
,∴![]() ,
,
④當![]() 時,
時,![]() 在
在![]() 單調(diào)遞增,在
單調(diào)遞增,在![]() 單調(diào)遞減,滿足條件,
單調(diào)遞減,滿足條件,
綜上所述:![]() 時,存在
時,存在![]() ,使得
,使得![]() 是
是![]() 在
在![]() 上的最大值.
上的最大值.
(2)![]() 對任意
對任意![]() 恒成立,
恒成立,
即![]() 對任意
對任意![]() 恒成立,令
恒成立,令
![]() ,
,![]() ,根據(jù)題意,可以知道
,根據(jù)題意,可以知道![]() 的最大值為1,則
的最大值為1,則
![]() 恒成立,
恒成立,
由于![]() ,則
,則![]() ,
,
當![]() 時,
時,![]() ,則
,則![]() ,若
,若![]() ,則
,則![]() 在
在![]() 上遞減,在
上遞減,在![]() 上遞增,則
上遞增,則![]() ,∴
,∴![]() 在
在![]() 上是遞增的函數(shù).
上是遞增的函數(shù).
∴![]() ,滿足條件,∴
,滿足條件,∴![]() 的取值范圍是
的取值范圍是![]() .
.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() ,橢圓
,橢圓![]() 的離心率為
的離心率為![]() ,
, ![]() 是橢圓
是橢圓![]() 的右焦點,
的右焦點, ![]() 的斜率為
的斜率為![]() ,
, ![]() 為坐標原點.
為坐標原點.
(1)求橢圓![]() 的方程;
的方程;
(2)設(shè)過點![]() 的動直線
的動直線![]() 與
與![]() 交于
交于![]() ,
, ![]() 兩點,當
兩點,當![]() 面積最大時,求
面積最大時,求![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】《中國好聲音(![]()
![]()
![]()
![]() )》是由浙江衛(wèi)視聯(lián)合星空傳媒旗下燦星制作強力打造的大型勵志專業(yè)音樂評論節(jié)目,于2012年7月13日在浙江衛(wèi)視播出.每期節(jié)目有四位導(dǎo)師參加.導(dǎo)師背對歌手,當每位參賽選手演唱完之前有導(dǎo)師為其轉(zhuǎn)身,則該選手可以選擇加入為其轉(zhuǎn)身的導(dǎo)師的團隊中接受指導(dǎo)訓(xùn)練.已知某期《中國好聲音》中,6位選手唱完后,四位導(dǎo)師為其轉(zhuǎn)身的情況如下表所示:
)》是由浙江衛(wèi)視聯(lián)合星空傳媒旗下燦星制作強力打造的大型勵志專業(yè)音樂評論節(jié)目,于2012年7月13日在浙江衛(wèi)視播出.每期節(jié)目有四位導(dǎo)師參加.導(dǎo)師背對歌手,當每位參賽選手演唱完之前有導(dǎo)師為其轉(zhuǎn)身,則該選手可以選擇加入為其轉(zhuǎn)身的導(dǎo)師的團隊中接受指導(dǎo)訓(xùn)練.已知某期《中國好聲音》中,6位選手唱完后,四位導(dǎo)師為其轉(zhuǎn)身的情況如下表所示:
導(dǎo)師轉(zhuǎn)身人數(shù)(人) | 4 | 3 | 2 | 1 |
獲得相應(yīng)導(dǎo)師轉(zhuǎn)身的選手人數(shù)(人) | 1 | 2 | 2 | 1 |
現(xiàn)從這6位選手中隨機抽取兩人考查他們演唱完后導(dǎo)師的轉(zhuǎn)身情況.
(1)請列出所有的基本事件;
(2)求兩人中恰好其中一位為其轉(zhuǎn)身的導(dǎo)師不少于3人,而另一人為其轉(zhuǎn)身的導(dǎo)師不多于2人的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() ,函數(shù)
,函數(shù)![]() .
.
(1)求證:曲線![]() 在點
在點![]() 處的切線過定點;
處的切線過定點;
(2)若![]() 是
是![]() 在區(qū)間
在區(qū)間![]() 上的極大值,但不是最大值,求實數(shù)
上的極大值,但不是最大值,求實數(shù)![]() 的取值范圍;
的取值范圍;
(3)求證:對任意給定的正數(shù)![]() ,總存在
,總存在![]() ,使得
,使得![]() 在
在![]() 上為單調(diào)函數(shù).
上為單調(diào)函數(shù).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)等差數(shù)列![]() 是無窮數(shù)列,且各項均為互不相同的正整數(shù),其前
是無窮數(shù)列,且各項均為互不相同的正整數(shù),其前![]() 項和為
項和為![]() ,數(shù)列
,數(shù)列![]() 滿足
滿足![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若數(shù)列![]() 為等差數(shù)列,求
為等差數(shù)列,求![]() ;
;
(3)在(1)的條件下,求證:數(shù)列![]() 中存在無窮多項(按原來的順序)成等比數(shù)列.
中存在無窮多項(按原來的順序)成等比數(shù)列.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某校男女籃球隊各有10名隊員,現(xiàn)將這20名隊員的身高繪制成莖葉圖(單位:![]() ).男隊員身高在
).男隊員身高在![]() 以上定義為“高個子”,女隊員身高在
以上定義為“高個子”,女隊員身高在![]() 以上定義為“高個子”,其他隊員定義為“非高個子”,按照“高個子”和“非高個子”用分層抽樣的方法共抽取5名隊員.
以上定義為“高個子”,其他隊員定義為“非高個子”,按照“高個子”和“非高個子”用分層抽樣的方法共抽取5名隊員.
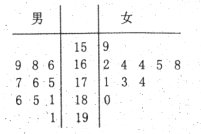
(1)從這5名隊員中隨機選出2名隊員,求這2名隊員中有“高個子”的概率;
(2)求這5名隊員中,恰好男女“高個子”各1名隊員的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)求![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)若![]() 在
在![]() 上的最大值是
上的最大值是![]() ,求
,求![]() 的值;
的值;
(3)記![]() ,當
,當![]() 時,若對任意
時,若對任意![]() ,總有
,總有![]() 成立,試求
成立,試求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)若![]() ,判斷函數(shù)
,判斷函數(shù)![]() 的單調(diào)性;
的單調(diào)性;
(2)若函數(shù)![]() 在定義域內(nèi)單調(diào)遞減,求實數(shù)
在定義域內(nèi)單調(diào)遞減,求實數(shù)![]() 的取值范圍;
的取值范圍;
(3)當![]() 時,關(guān)于
時,關(guān)于![]() 的方程
的方程![]() 在
在![]() 上恰有兩個不相等的實數(shù)根,求實數(shù)
上恰有兩個不相等的實數(shù)根,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com