
分析 如圖所示,設(shè)△ABC的內(nèi)切圓的半徑r=1.在△BOD中,$\frac{BC}{2}$=BD=$\frac{OD}{tan30°}$,即可得出.
解答 解:如圖所示,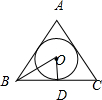
設(shè)△ABC的內(nèi)切圓與邊BC相切于點D,其圓心為O點,半徑r=1.
連接OB,則OB平分∠ABC,∴∠OBD=30°.
在△BOD中,$\frac{BC}{2}$=BD=$\frac{OD}{tan30°}$=$\frac{1}{\frac{\sqrt{3}}{3}}$,
解得BC=2$\sqrt{3}$.
∵圓中一段弧長正好等于該圓的外切正三角形的邊長,
∴這段弧所對的圓心角的弧度數(shù)為2$\sqrt{3}$.
故答案為:$2\sqrt{3}$.
點評 本題考查了三角形的內(nèi)切圓的性質(zhì)、正三角形的性質(zhì)、含30°角的直角三角形的邊角關(guān)系,屬于基礎(chǔ)題.


科目:高中數(shù)學 來源: 題型:選擇題
| A. | e2 | B. | $\frac{{{e^2}+1}}{2}$ | C. | $\frac{{{e^2}-1}}{2}$ | D. | $\frac{{{e^2}+3}}{2}$ |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:選擇題
| A. | (-1,3) | B. | [-2,1) | C. | {0,1,2} | D. | {-2,-1,0} |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
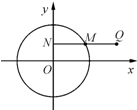 如圖,已知點M在圓O:x2+y2=4上運動,MN⊥y軸(垂足為N),點Q在NM的延長線上,且|QN|=2|MN|.
如圖,已知點M在圓O:x2+y2=4上運動,MN⊥y軸(垂足為N),點Q在NM的延長線上,且|QN|=2|MN|.查看答案和解析>>
科目:高中數(shù)學 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com