Question

1．設點P在曲線y=$\frac{1}{2}$x²上，從原點向A（2，2）移動，如果直線OP，曲線y=$\frac{1}{2}$x²及直線x=2所圍成的陰影部分面積分別記為S₁、S₂．
（Ⅰ）當S₁=S₂時，求點P的坐標；
（Ⅱ）當S₁+S₂有最小值時，求點P的坐標和最小值．

Answer 1

分析 （Ⅰ）可考慮用定積分求兩曲線圍成的封閉圖形面積，直線OP的方程為y=$\frac{1}{2}$tx，則S₁為直線OP與曲線y=$\frac{1}{2}$x²當x∈（0，t）時所圍面積，所以，S₁=∫₀^t（$\frac{1}{2}$tx-$\frac{1}{2}$x²）dx，S₂為直線OP與曲線y=$\frac{1}{2}$x²當x∈（t，2）時所圍面積，所以S₂=∫_t²（$\frac{1}{2}$x²-$\frac{1}{2}$tx）dx，再根據S₁=S₂就可求出t值．
（Ⅱ）由（Ⅰ）可求當S₁+S₂，化簡后，為t的三次函數，再利用導數求最小值，以及相應的x值，就可求出P點坐標為多少時，S₁+S₂有最小值．

解答 解：（Ⅰ）設點p的橫坐標為t（0＜t＜2），
則P點的坐標為（t，$\frac{1}{2}$t²），
直線OP的方程為y=$\frac{1}{2}$tx，
s₁=${∫}_{0}^{t}$（$\frac{1}{2}$tx-$\frac{1}{2}$x²）dx=$\frac{1}{12}$t³，S₂=${∫}_{t}^{2}$（$\frac{1}{2}$x²-$\frac{1}{2}$tx）dx=$\frac{1}{12}$t³-t+$\frac{4}{3}$，
因為S₁=S₂，所以t=$\frac{4}{3}$，點P的坐標為（$\frac{4}{3}$，$\frac{8}{9}$）．
（Ⅱ）S=S₁+S₂=$\frac{1}{12}$t³+$\frac{1}{12}$t³-t+$\frac{4}{3}$=$\frac{1}{6}$t³-t+$\frac{4}{3}$，
S′=$\frac{1}{2}$t²-1，令S′=0，得$\frac{1}{2}$t²-1=0，∴t=$\sqrt{2}$，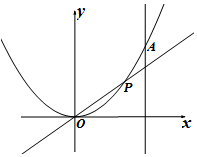

因為9＜t＜$\sqrt{2}$時，S′＜0；$\sqrt{2}$＜t＜2時，S′＞0，
所以，當t=$\sqrt{2}$時，S_min=$\frac{4-2\sqrt{2}}{3}$，
P點的坐標為（$\sqrt{2}$，1）．

點評 本題考查了用定積分求兩曲線所圍圖形面積，以及導數求最值，做題時應認真分析．