
分析 (1)根據對數的運算解不等式即可.
(2)根據f(0)=1,求f(x)的解析式,根據$f(x)={(\frac{1}{{\sqrt{2}}})^x}+λ$在閉區間[2,3]上有實數解,分離λ,可得λ=lg(x+10)-$(\frac{1}{\sqrt{2}})^{x}$,令F(x)=lg(x+10)-$(\frac{1}{\sqrt{2}})^{x}$,求在閉區間[2,3]上的值域即為λ的范圍.
(3)函數f(x)的圖象過點(98,2),求f(x)的解析式,可得f(x)=lg(2+x)那么:不等式f[cos(2nx)]<lg2轉化為lg(2+cos(2nx))<lg2轉化為$\left\{\begin{array}{l}{2+cos({2}^{n}x)>0}\\{cos({2}^{n}x)<0}\end{array}\right.$,求解x,又∵2+x>0,即x>-2和n∈N.討論k的范圍可得答案.
解答 解:函數f(x)=lg(x+m)(m∈R);
(1)當m=2時,f(x)=lg(x+2)
那么:不等式$f(\frac{1}{x})>1$;即lg($\frac{1}{x}$+2)>lg10,
可得:$\frac{1}{x}+2>10$,且$\frac{1}{x}+2>0$
解得:$0<x<\frac{1}{8}$.
∴不等式的解集為{x|$0<x<\frac{1}{8}$}
(2)∵f(0)=1,可得m=10.
∴f(x)=lg(x+10)
$f(x)={(\frac{1}{{\sqrt{2}}})^x}+λ$,即lg(x+10)=$(\frac{1}{\sqrt{2}})^{x}+λ$在閉區間[2,3]上有實數解,
可得λ=lg(x+10)-$(\frac{1}{\sqrt{2}})^{x}$
令F(x)=lg(x+10)-$(\frac{1}{\sqrt{2}})^{x}$,求在閉區間[2,3]上的值域.
根據指數和對數的性質可知:F(x)是增函數,
∴F(x)在閉區間[2,3]上的值域為[lg12-$\frac{1}{2}$,lg13-$\frac{\sqrt{2}}{4}$]
故得實數λ的范圍是[lg12-$\frac{1}{2}$,lg13-$\frac{\sqrt{2}}{4}$].
(3)∵函數f(x)的圖象過點(98,2),
則有:2=lg(98+m)
∴m=2.
故f(x)=lg(2+x)
那么:不等式f[cos(2nx)]<lg2轉化為lg(2+cos(2nx))<lg2
即cos(2nx)<0對n∈N均成立,
若x是滿足條件的實數,則有cosx≤-$\frac{1}{4}$,
因為,若-$\frac{1}{4}$<cosx<0,則cos2x=2cos2x-1<-$\frac{7}{8}$,則cos4x=2cos22x-1>0,
所以必有cos(2nx)≤-$\frac{1}{4}$;
得|cos(2nx)-$\frac{1}{2}$|≥$\frac{3}{4}$,又|cos2x+$\frac{1}{2}$|=2|cosx+$\frac{1}{2}$||cosx-$\frac{1}{2}$|≥$\frac{3}{2}$|cosx+$\frac{1}{2}$|,
得|cosx+$\frac{1}{2}$|≤$\frac{2}{3}$|cos2x+$\frac{1}{2}$|,重復運用得到|cosx+$\frac{1}{2}$|≤…≤$(\frac{2}{3})^{n}$|cos(2nx)+$\frac{1}{2}$|<$(\frac{2}{3})^{n}$
n為自然數,∴cosx+$\frac{1}{2}$=0,
級x=2kπ±$\frac{2π}{3}$,k∈Z.
驗證,當x=2kπ±$\frac{2π}{3}$,k∈Z時,有cos(2nx)=-$\frac{1}{2}$,滿足題意.
所以,x的取值范圍為{x|x=2kπ±$\frac{2π}{3}$,k∈Z}
點評 本題考查了對數的性質及其運算以及不等式恒成立的問題在對數與三角函數中的運用.有點難度.


 步步高達標卷系列答案
步步高達標卷系列答案科目:高中數學 來源: 題型:選擇題
| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{5}{6}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
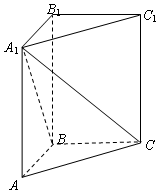 在正三棱柱ABC-A1B1C1中,AB=1,BB1=2,求:
在正三棱柱ABC-A1B1C1中,AB=1,BB1=2,求:查看答案和解析>>
科目:高中數學 來源: 題型:解答題
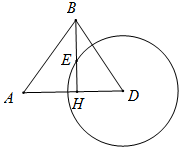 如圖,我海監船在D島海域例行維權巡航,某時刻航行至A處,此時測得其北偏東30°方向與它相距20海里的B處有一外國船只,且D島位于海監船正東18海里處.
如圖,我海監船在D島海域例行維權巡航,某時刻航行至A處,此時測得其北偏東30°方向與它相距20海里的B處有一外國船只,且D島位于海監船正東18海里處.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com