
分析 (1)根據題意,要求取出的4件產品沒有一等品,即在3件二等品、2件三等品中任取4件,由組合數公式計算可得答案;
(2)根據題意,分3種情況討論:①、取出的4件產品中有2件一等品、1件二等品、1件三等品,②、取出的4件產品中有1件一等品、2件二等品、1件三等品,③、取出的4件產品中有1件一等品、1件二等品、2件三等品,分別求出每一種情況的取法數目,由分類計數原理計算可得答案.
解答 解:(1)根據題意,有8件產品,其中一等品3件,二等品3件,三等品2件,
沒有一等品,即在3件二等品、2件三等品中任取4件即可,
有C54=5種取法,
則沒有一等品的不同抽法有5種,
(2)根據題意,分3種情況討論:
①、取出的4件產品中有2件一等品、1件二等品、1件三等品,有C32C31C21=18種取法;
②、取出的4件產品中有1件一等品、2件二等品、1件三等品,有C31C32C21=18種取法;
③、取出的4件產品中有1件一等品、1件二等品、2件三等品,有C31C31C22=9種取法;
則不同的取法有18+18+9=45種;
故一等品,二等品,三等品至少一件的不同抽法有45種.
點評 本題考查排列、組合的實際應用,(2)注意要分情況討論,要不重不漏.


科目:高中數學 來源: 題型:選擇題
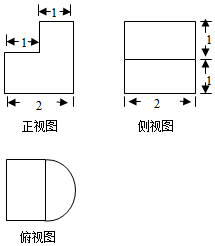
| A. | $\frac{1}{2}+\frac{π}{2}$ | B. | $1+\frac{π}{2}$ | C. | 1+π | D. | 2+π |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com