
【題目】某汽車制造廠制造了某款汽車.為了了解汽車的使用情況,通過問卷的形式,隨機對50名客戶對該款汽車的喜愛情況進行調查,如圖1是汽車使用年限的調查頻率分布直方圖,如表2是該50名客戶對汽車的喜愛情況.
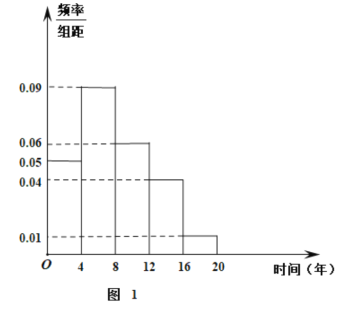
表2
不喜歡該款汽車 | 喜歡該款汽車 | 總計 | |
女士 | 11 | ||
男士 | 23 | 30 | |
總計 |
(1)將表2補充完整,并判斷能否在犯錯誤的概率不超過0.025的前提下認為是否喜歡該款汽車與性別有關;
(2)根據圖中的數據,甲說:“中位數在![]() 組內”;乙說:“平均數大于中位數”;丙說:“中位數和平均數一樣”,針對三位同學的說法,你認為哪種說法合理,給出說明.
組內”;乙說:“平均數大于中位數”;丙說:“中位數和平均數一樣”,針對三位同學的說法,你認為哪種說法合理,給出說明.
附:![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 寒假學與練系列答案
寒假學與練系列答案科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,以原點
中,以原點![]() 為極點,
為極點,![]() 軸正半軸為極軸建立極坐標系.已知直線
軸正半軸為極軸建立極坐標系.已知直線![]() 的極坐標方程為
的極坐標方程為![]() ,曲線
,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)寫出直線![]() 和曲線
和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)過動點![]() 且平行于
且平行于![]() 的直線交曲線
的直線交曲線![]() 于
于![]() 兩點,若
兩點,若![]() ,求動點
,求動點![]() 到直線
到直線![]() 的最近距離.
的最近距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】目前,新冠病毒引發的肺炎疫情在全球肆虐,為了止損,某地一水果店老板利用抖音直播賣貨,經過一段時間對一種水果的銷售情況進行統計,得到![]() 天的數據如下:
天的數據如下:
銷售單價 |
|
|
|
|
|
銷售量 |
|
|
|
|
|
(1)建立![]() 關于
關于![]() 的回歸直線方程;
的回歸直線方程;
(2)該水果店開展促銷活動,當該水果銷售單價為![]() 元/
元/![]() 時,其銷售量達到
時,其銷售量達到![]() ,若由回歸直線方程得到的預測數據與此次促銷活動的實際數據之差的絕對值不超過
,若由回歸直線方程得到的預測數據與此次促銷活動的實際數據之差的絕對值不超過![]() ,則認為所得到的回歸直線方程是理想的,試問:(1)中得到的回歸直線方程是否理想?
,則認為所得到的回歸直線方程是理想的,試問:(1)中得到的回歸直線方程是否理想?
(3)根據(1)的結果,若該水果成本是![]() 元/
元/![]() ,銷售單價
,銷售單價![]() 為何值時(銷售單價不超過
為何值時(銷售單價不超過![]() 元/
元/![]() ),該水果店利潤的預計值最大?
),該水果店利潤的預計值最大?
參考公式:回歸直線方程![]() ,其中
,其中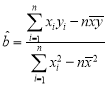 ,
,![]() .
.
參考數據:![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年12月12日我國出現了新型冠狀病毒所感染的肺炎,新型冠狀病毒的傳染性極強.下圖是2020年1月26號到2月17號全國/湖北/非湖北新增新型冠狀病毒感染確診病例對比圖,根據圖象下列判斷錯誤的是( )
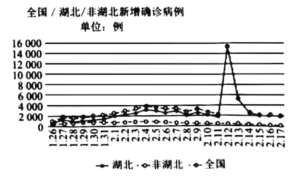
A.該時段非湖北新增感染確診病例比湖北少
B.全國新增感染確診病例平均數先增后減
C.2.12全國新增感染確診病例明顯增加,主要是由湖北引起的
D.2.12全國新增感染確診病例數突然猛增,不會影響該段時期全國新增病例數的中位數
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某化工廠在定期檢修設備時發現生產管道中共有5處閥門(![]() )發生有害氣體泄漏.每處閥門在每小時內有害氣體的泄露量大體相等,約為0.01立方米.閥門的修復工作可在不停產的情況下實施.由于各閥門所處的位置不同,因此修復所需的時間不同,且修復時必須遵從一定的順序關系,具體情況如下表:
)發生有害氣體泄漏.每處閥門在每小時內有害氣體的泄露量大體相等,約為0.01立方米.閥門的修復工作可在不停產的情況下實施.由于各閥門所處的位置不同,因此修復所需的時間不同,且修復時必須遵從一定的順序關系,具體情況如下表:
泄露閥門 |
|
|
|
|
|
修復時間 (小時) | 11 | 8 | 5 | 9 | 6 |
需先修復 好的閥門 |
|
|
|
|
|
在只有一個閥門修復設備的情況下,合理安排修復順序,泄露的有害氣體總量最小為( )
A.1.14立方米B.1.07立方米C.1.04立方米D.0.39立方米
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在正方體![]() 中,點E是棱
中,點E是棱![]() 的中點,點F是線段
的中點,點F是線段![]() 上的一個動點.有以下三個命題:
上的一個動點.有以下三個命題:
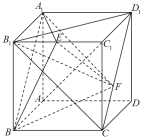
①異面直線![]() 與
與![]() 所成的角是定值;
所成的角是定值;
②三棱錐![]() 的體積是定值;
的體積是定值;
③直線![]() 與平面
與平面![]() 所成的角是定值.
所成的角是定值.
其中真命題的個數是( )
A. 3 B. 2 C. 1 D. 0
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com