
【題目】在平面直角坐標(biāo)系![]() 中,以原點
中,以原點![]() 為極點,
為極點,![]() 軸正半軸為極軸建立極坐標(biāo)系.已知直線
軸正半軸為極軸建立極坐標(biāo)系.已知直線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() ,曲線
,曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(1)寫出直線![]() 和曲線
和曲線![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(2)過動點![]() 且平行于
且平行于![]() 的直線交曲線
的直線交曲線![]() 于
于![]() 兩點,若
兩點,若![]() ,求動點
,求動點![]() 到直線
到直線![]() 的最近距離.
的最近距離.
【答案】(1)直線![]() :
:![]() ;曲線
;曲線![]() :
:![]() ;(2)
;(2)![]() .
.
【解析】
(1)運用極坐標(biāo)和直角坐標(biāo)的關(guān)系,以及兩角差的正弦公式,化簡可得所求直角坐標(biāo)方程;
(2)設(shè)出過![]() 且平行于
且平行于![]() 的直線的參數(shù)方程,代入拋物線方程,化簡整理,運用韋達(dá)定理和參數(shù)的幾何意義,運用點到直線的距離公式和二次函數(shù)的最值求法,可得所求最值.
的直線的參數(shù)方程,代入拋物線方程,化簡整理,運用韋達(dá)定理和參數(shù)的幾何意義,運用點到直線的距離公式和二次函數(shù)的最值求法,可得所求最值.
(1)直線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() ,即為
,即為![]() ,
,
即![]() ,可得
,可得![]() ,即
,即![]() ;
;
曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() ,即為
,即為![]() ,
,
可得![]() ;
;
(2)設(shè)過點![]() 且平行于
且平行于![]() 的直線的參數(shù)方程設(shè)為
的直線的參數(shù)方程設(shè)為 (
(![]() 為參數(shù)),
為參數(shù)),
代入拋物線方程![]() ,可得
,可得 ,
,
設(shè)![]() 對應(yīng)的參數(shù)分別為
對應(yīng)的參數(shù)分別為![]() ,可得
,可得![]() ,
,
又![]() ,即有
,即有![]() ,
,
由![]() ,可得
,可得![]() ,即
,即![]() ,
,
![]() 到直線
到直線![]() 的距離:
的距離:
 ,
,
當(dāng)![]() ,
,![]() 時,動點
時,動點![]() 到直線
到直線![]() 的最近距離為
的最近距離為![]() .
.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】在△ABC中,a![]() ,c
,c![]() ,________.(補(bǔ)充條件)
,________.(補(bǔ)充條件)
(1)求△ABC的面積;
(2)求sin(A+B).
從①b=4,②cosB![]() ,③sinA
,③sinA![]() 這三個條件中任選一個,補(bǔ)充在上面問題中并作答.
這三個條件中任選一個,補(bǔ)充在上面問題中并作答.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】2020年1月22日,國新辦發(fā)布消息:新型冠狀病毒來源于武漢一家海鮮市場非法銷售的野生動.專家通過全基因組比對發(fā)現(xiàn)此病毒與2003年的非典冠狀病毒以及此后的中東呼吸綜合征冠狀病毒,分別達(dá)到70%和40%的序列相似性.這種新型冠狀病毒對人們的健康生命帶來了嚴(yán)重威脅因此,某生物疫苗研究所加緊對新型冠狀病毒疫苗進(jìn)行實驗,并將某一型號疫苗用在動物小白鼠身上進(jìn)行科研和臨床實驗,得到統(tǒng)計數(shù)據(jù)如下:
未感染病毒 | 感染病毒 | 總計 | |
未注射疫苗 | 20 |
|
|
注射疫苗 | 30 |
|
|
總計 | 50 | 50 | 100 |
現(xiàn)從所有試驗小白鼠中任取一只,取到“注射疫苗”小白鼠的概率為![]() .
.
(1)求![]() 列聯(lián)表中的數(shù)據(jù)
列聯(lián)表中的數(shù)據(jù)![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
(2)能否有99.9%把握認(rèn)為注射此種疫苗對預(yù)防新型冠狀病毒有效?
附:![]() .
.
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知定義在![]() 上的函數(shù)
上的函數(shù)![]() 滿足
滿足![]() ,當(dāng)
,當(dāng)![]() 時
時![]() ,則關(guān)于函數(shù)
,則關(guān)于函數(shù)![]() 有如下四個結(jié)論:①
有如下四個結(jié)論:①![]() 為偶函數(shù);②
為偶函數(shù);②![]() 的圖象關(guān)于直線
的圖象關(guān)于直線![]() 對稱;③方程
對稱;③方程![]() 有兩個不等實根;④
有兩個不等實根;④![]() 其中所有正確結(jié)論的編號是_______.
其中所有正確結(jié)論的編號是_______.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知直線![]() 過橢圓
過橢圓![]() 的右焦點,且交橢圓于A,B兩點,線段AB的中點是
的右焦點,且交橢圓于A,B兩點,線段AB的中點是![]() ,
,
(1)求橢圓的方程;
(2)過原點的直線l與線段AB相交(不含端點)且交橢圓于C,D兩點,求四邊形![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,令
,令![]() ,其中
,其中![]() 是函數(shù)
是函數(shù)![]() 的導(dǎo)函數(shù).
的導(dǎo)函數(shù).
(Ⅰ)當(dāng)![]() 時,求
時,求![]() 的極值;
的極值;
(Ⅱ)當(dāng)![]() 時,若存在
時,若存在![]() ,使得
,使得![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】過點![]() 的動直線l與y軸交于點
的動直線l與y軸交于點![]() ,過點T且垂直于l的直線
,過點T且垂直于l的直線![]() 與直線
與直線![]() 相交于點M.
相交于點M.
(1)求M的軌跡方程;
(2)設(shè)M位于第一象限,以AM為直徑的圓![]() 與y軸相交于點N,且
與y軸相交于點N,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
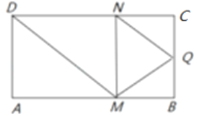
【題目】如圖,矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 為
為![]() 的中點,點
的中點,點![]() ,
,![]() 分別在線段
分別在線段![]() ,
,![]() 上運動(其中
上運動(其中![]() 不與
不與![]() ,
,![]() 重合,
重合,![]() 不與
不與![]() ,
,![]() 重合),且
重合),且![]() ,沿
,沿![]() 將
將![]() 折起,得到三棱錐
折起,得到三棱錐![]() ,則三棱錐
,則三棱錐![]() 體積的最大值為______;當(dāng)三棱錐
體積的最大值為______;當(dāng)三棱錐![]() 體積最大時,其外接球的半徑
體積最大時,其外接球的半徑![]() ______.
______.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com