
【題目】已知函數![]() ,令
,令![]() ,其中
,其中![]() 是函數
是函數![]() 的導函數.
的導函數.
(Ⅰ)當![]() 時,求
時,求![]() 的極值;
的極值;
(Ⅱ)當![]() 時,若存在
時,若存在![]() ,使得
,使得![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
【答案】(Ⅰ) 極小值![]() ,無極大值;(Ⅱ)
,無極大值;(Ⅱ)![]() .
.
【解析】
試題分析:(Ⅰ)把![]() 代入函數
代入函數![]() 的解析式,求其導函數,由導函數的零點對定義域分段,得到函
的解析式,求其導函數,由導函數的零點對定義域分段,得到函
數在各區間段內的單調性,從而求得函數極值;(Ⅱ)由函數的導函數可得函數的單調性,求得函數在![]() 上的最值,再由
上的最值,再由![]() 恒成立,結合分離參數可得
恒成立,結合分離參數可得![]() ,構造函數
,構造函數![]() ,利用導數求其最值得
,利用導數求其最值得![]() 的范圍.
的范圍.
試題解析:(Ⅰ)依題意![]() ,則
,則![]()
當a=0時,![]()
令![]() 解得
解得![]() ;
;
當![]() 時,
時,![]() ,當
,當![]() 時,
時,![]()
所以![]() 的單調遞減區間為(0,
的單調遞減區間為(0,![]() ),單調遞增區間為(
),單調遞增區間為(![]() ,+∞)
,+∞)
所以![]() 時
時![]() 取得極小值
取得極小值![]() ,無極大值.
,無極大值.
(Ⅱ)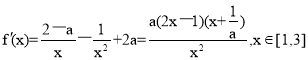
當![]() 即
即![]() 時,恒有
時,恒有![]() 成立,
成立,
所以![]() 在[1,3]上是單調遞減.
在[1,3]上是單調遞減.
所以![]()
所以![]() ,
,
因為存在![]() ,使得
,使得![]() 恒成立,
恒成立,
所以![]() 整理得
整理得
![]()
又![]() <0,所以
<0,所以![]()
令![]() =-
=-![]() ,則
,則![]() ∈(2,8),構造函數
∈(2,8),構造函數![]() ,
,
所以![]() ,
,
當![]() 時,
時,![]() ,當
,當![]() 時,
時,![]() ,此時函數單調遞增,
,此時函數單調遞增,
當![]() 時,
時,![]() ,此時函數單調遞減,
,此時函數單調遞減,
所以![]() ,
,
所以m的取值范圍為(![]() ,+∞).
,+∞).


科目:高中數學 來源: 題型:
【題目】(1)已知函數f(x)(x∈R)是奇函數,且當x>0時,f(x)=2x-1,求函數f(x)的解析式.
(2)已知x+y=12,xy=9且x<y,求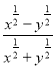 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合P={x|a+1≤x≤2a+1},Q={x|1≤2x+5≤15}.
(1)已知a=3,求(RP)∩Q;
(2)若P∪Q=Q,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)若![]() 對
對![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍;
的取值范圍;
(2)是否存在整數![]() ,使得函數
,使得函數![]() 在區間
在區間![]() 上存在極小值,若存在,求出所有整數
上存在極小值,若存在,求出所有整數![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的右焦點
的右焦點![]() ,橢圓
,橢圓![]() 的左,右頂點分別為
的左,右頂點分別為![]() .過點
.過點![]() 的直線
的直線![]() 與橢圓交于
與橢圓交于![]() 兩點,且
兩點,且![]() 的面積是
的面積是![]() 的面積的3倍.
的面積的3倍.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)若![]() 與
與![]() 軸垂直,
軸垂直,![]() 是橢圓
是橢圓![]() 上位于直線
上位于直線![]() 兩側的動點,且滿足
兩側的動點,且滿足![]() ,試問直線
,試問直線![]() 的斜率是否為定值,請說明理由.
的斜率是否為定值,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
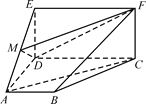
【題目】如圖,四邊形ABCD是梯形,四邊形CDEF是矩形,且平面ABCD⊥平面CDEF,∠BAD=∠CDA=90°,![]() ,M是線段AE上的動點.
,M是線段AE上的動點.
(1)試確定點M的位置,使AC∥平面DMF,并說明理由;
(2)在(1)的條件下,求平面DMF與平面ABCD所成銳二面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2017年春節期間,某服裝超市舉辦了一次有獎促銷活動,消費每超過600元(含600元),均可抽獎一次,抽獎方案有兩種,顧客只能選擇其中的一種.
方案一:從裝有10個形狀、大小完全相同的小球(其中紅球3個,黑球7個)的抽獎盒中,一次性摸出3個球,其中獎規則為:若摸到3個紅球,享受免單優惠;若摸出2個紅球則打6折,若摸出1個紅球,則打7折;若沒摸出紅球,則不打折.
方案二:從裝有10個形狀、大小完全相同的小球(其中紅球3個,黑球7個)的抽獎盒中,有放回每次摸取1球,連摸3次,每摸到1次紅球,立減200元.
(1)若兩個顧客均分別消費了600元,且均選擇抽獎方案一,試求兩位顧客均享受免單優惠的概率;
(2)若某顧客消費恰好滿1000元,試從概率的角度比較該顧客選擇哪一種抽獎方案更合算?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】第![]() 屆夏季奧林匹克運動會將于 2016 年 8 月 5 日—21 日在巴西里約熱內盧舉行.下表是近五屆奧運會中國代表團和俄羅斯代表團獲得的金牌數的統計數據( 單位: 枚).
屆夏季奧林匹克運動會將于 2016 年 8 月 5 日—21 日在巴西里約熱內盧舉行.下表是近五屆奧運會中國代表團和俄羅斯代表團獲得的金牌數的統計數據( 單位: 枚).
第 | 第 | 第 | 第 | 第 | |
中國 |
|
|
|
|
|
俄羅斯 |
|
|
|
|
|
(1)根據表格中兩組數據完成近五屆奧運會兩國代表團獲得的金牌數的莖葉圖, 并通過莖葉圖比較兩國代表團獲得的金牌數的平均值及分散程度( 不要求計算出具體數值, 給出結論即可);
(2)甲、 乙、 丙三人競猜今年中國代表團和俄羅斯代表團中的哪一個獲得的金牌數多( 假設兩國代表團獲得的金牌數不會相等) , 規定甲、 乙、 丙必須在兩個代表團中選一個, 已知甲、 乙猜中國代表團的概率都為![]() , 丙猜中國代表團的概率為
, 丙猜中國代表團的概率為![]() , 三人各自猜哪個代表團的結果互不影響.現讓甲、 乙、 丙各猜一次, 設三人中猜中國代表團的人數為
, 三人各自猜哪個代表團的結果互不影響.現讓甲、 乙、 丙各猜一次, 設三人中猜中國代表團的人數為![]() ,求
,求![]() 的分布列及數學期望
的分布列及數學期望![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com