
分析 (1)利用已知條件求出b,c即可推出函數的解析式.
(2)g(x)=f(x)-|x-1|表示為分段函數的形式,然后求解最小值.
解答 (1)解:∵f(0)=0,∴c=0.…(2分)
∵對于任意x∈R都有,f(-1-x)=f(x)
∴函數f(x)的對稱軸為$x=-\frac{1}{2}$,即b=1.…(4分)
∴f(x)=x2+x.----(6分)
(2)$g(x)=\left\{{\begin{array}{l}{{x^2}+1(x≥1)}\\{{x^2}+2x-1(x<1)}\end{array}}\right.$-------(8分)
當x≥1時 g(x)=x2+1 函數的最小值為2
當x<1時 g(x)=x2+2x-1 函數的最小值為1-------(11分)
所以函數的最小值為1-------------(12分)
點評 本題考查二次函數的性質,函數的解析式的求法,分段函數的應用,考查計算能力.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
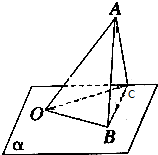 如圖所示,已知∠BOC在平面α內,OA是平面α的斜線,且∠AOB=∠AOC=60°,OA=OB=OC=a,BC=$\sqrt{2}$a,求OA和平面α所成的角.
如圖所示,已知∠BOC在平面α內,OA是平面α的斜線,且∠AOB=∠AOC=60°,OA=OB=OC=a,BC=$\sqrt{2}$a,求OA和平面α所成的角.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
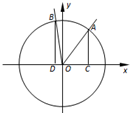 在平面直角坐標系xOy中,角α的頂點是坐標原點,始邊為x軸的正半軸,終邊與單位圓O交于點A(x1,y1),α∈($\frac{π}{4}$,$\frac{π}{2}$).將角α終邊繞原點按逆時針方向旋轉$\frac{π}{4}$,交單位圓于點B(x2,y2).過A,B作x軸的垂線,垂足分別為C,D,記△AOC及△BOD的面積分別為S1,S2,且S1=$\frac{4}{3}$S2,則tanα的值等于( )
在平面直角坐標系xOy中,角α的頂點是坐標原點,始邊為x軸的正半軸,終邊與單位圓O交于點A(x1,y1),α∈($\frac{π}{4}$,$\frac{π}{2}$).將角α終邊繞原點按逆時針方向旋轉$\frac{π}{4}$,交單位圓于點B(x2,y2).過A,B作x軸的垂線,垂足分別為C,D,記△AOC及△BOD的面積分別為S1,S2,且S1=$\frac{4}{3}$S2,則tanα的值等于( )| A. | 1 | B. | 2 | C. | $\frac{1}{2}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com