
分析 先求函數的導函數,找出導函數的零點,把定義域由零點分成幾個區間判斷導函數在各區間內的符號,從而得到原函數在個區間內的單調性;的單調區間,說明函數在區間(-2,-1)內單調遞增,在區間(-1,0)內單調遞減,結合函數零點和方程根的轉化列式可求a的范圍.
解答 解:由函數$f(x)=\frac{1}{3}{x^3}+\frac{1-a}{2}{x^2}-ax-a,x∈R$,得f′(x)=x2+(1-a)x-a=(x+1)(x-a)
由f′(x)=0,得x1=-1,x2=a>0.
當x∈(-∞,-1)時,f′(x)>0,f(x)為增函數,
當x∈(-1,a)時,f′(x)<0,f(x)為減函數,
當x∈(a,+∞)時,f′(x)>0,f(x)為增函數.
故函數f(x)的增區間是(-∞,-1),(a,+∞);減區間為(-1,a).
f(x)在區間(-2,-1)內單調遞增,在區間(-1,0)內單調遞減,
從而函數f(x)在區間(-2,0)內恰有兩個零點當且僅當$\left\{\begin{array}{l}{f(-2)<0}\\{f(-1)>0}\\{f(0)<0}\end{array}\right.$,
解得0<a<$\frac{1}{3}$.
所以a的取值范圍是(0,$\frac{1}{3}$).
故答案為:$({0,\frac{1}{3}})$.
點評 本題考查利用導數研究函數的單調性,考查分類討論的數學思想方法,會利用導數研究函數的單調區間以及根據函數的增減性得到函數的最值.掌握不等式恒成立時所取的條件.


 精英口算卡系列答案
精英口算卡系列答案科目:高中數學 來源: 題型:解答題
 如圖,四棱錐C-ABB1A1內接于圓柱OO1,且A1A,B1B都垂直于底面圓O,BC過底面圓心O,M,N分別是棱AA1,CB1的中點,MN⊥平面CBB1.
如圖,四棱錐C-ABB1A1內接于圓柱OO1,且A1A,B1B都垂直于底面圓O,BC過底面圓心O,M,N分別是棱AA1,CB1的中點,MN⊥平面CBB1.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
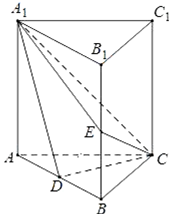 如圖,直三棱柱ABC-A1B1C1中,D,E分別是AB,BB1的中點,AA1=AC=CB=$\frac{\sqrt{2}}{2}$AB.
如圖,直三棱柱ABC-A1B1C1中,D,E分別是AB,BB1的中點,AA1=AC=CB=$\frac{\sqrt{2}}{2}$AB.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 2 | B. | $\sqrt{2}$ | C. | $\frac{{\sqrt{5}}}{2}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | [2,+∞]∪(-∞,$\frac{1}{2}$] | B. | (0,$\frac{1}{2}$]∪[2,+∞) | C. | [$\frac{1}{2}$,2] | D. | (0,$\frac{1}{2}$] |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
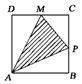 如圖所示,點P在邊長為1的正方形的邊上運動,設M是CD邊的中點,則當P沿著A-B-C-M運動時,以點P經過的路程x為自變量,三角形APM的面積為y的函數,則y=f(x)的圖象形狀大致是下列圖中的( )
如圖所示,點P在邊長為1的正方形的邊上運動,設M是CD邊的中點,則當P沿著A-B-C-M運動時,以點P經過的路程x為自變量,三角形APM的面積為y的函數,則y=f(x)的圖象形狀大致是下列圖中的( )| A. | 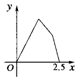 | B. | 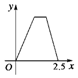 | C. | 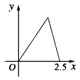 | D. | 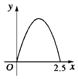 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com