
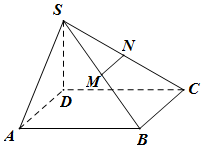
 已知四棱錐S-ABCD的底面為平行四邊形SD⊥面ABCD,SD=1,AB=2,AD=1,∠DAB=60°,M、N分別為SB、SC中點,過MN作平面MNPQ分別與線段CD、AB相交于點P、Q.
已知四棱錐S-ABCD的底面為平行四邊形SD⊥面ABCD,SD=1,AB=2,AD=1,∠DAB=60°,M、N分別為SB、SC中點,過MN作平面MNPQ分別與線段CD、AB相交于點P、Q.分析 (Ⅰ)取DC中點P,AB中點Q,連MQ、PQ、NP,則作出平面MNPQ,使面MNPQ∥面SAD.
(Ⅱ)由余弦定理求得$BD=2\sqrt{3}$,從而AD⊥BD,以D為原點,直線DA為x軸,直線DB為y軸,直線DS為z軸建立空間直角坐標系,利用向量法能求出二面角M-PQ-B的大小.
解答 解:(Ⅰ)如圖,P是DC的中點,Q是AB的中點,
取DC中點P,AB中點Q,連MQ、PQ、NP,則作出平面MNPQ,使面MNPQ∥面SAD.
(若NP.PQ未作成虛線,扣兩分)…(4分)
(Ⅱ)在平行四邊形ABCD中,設AB=2AD=4,∠DCB=60°,
所以由余弦定理得$BD=2\sqrt{3}$,有AB2=AD2+BD2,所以AD⊥BD,….(5分)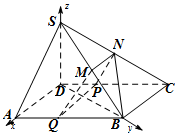 以D為原點,直線DA為x軸,直線DB為y軸,直線DS為z軸建立空間直角坐標系,
以D為原點,直線DA為x軸,直線DB為y軸,直線DS為z軸建立空間直角坐標系,
且$A({1,0,0}),B({0,\sqrt{3},0}),S({0,0,1}),M({0,\frac{{\sqrt{3}}}{2},\frac{1}{2}})$,
又$\overrightarrow{AQ}=\frac{1}{3}\overrightarrow{AB}$,設Q(x,y,z),則$Q({\frac{2}{3},\frac{{\sqrt{3}}}{3},0})$…(7分)
設平面的法向量為$\overrightarrow n=({x,y,z})$
由$\left\{{\begin{array}{l}{\overrightarrow n•\overrightarrow{AD}=0}\\{\overrightarrow n•\overrightarrow{MQ}=0}\end{array}}\right.$得$\overrightarrow n=({0,-\sqrt{3},1})$,…(9分)
易知面ABCD的法向量為$\overrightarrow m=({0,0,1})$
則$cos\left?{\vec m,\left.{\vec n}\right>}\right.=\frac{{|{\overrightarrow m\overrightarrow{•n}}|}}{{|{\overrightarrow m}||{\overrightarrow n}|}}=\frac{1}{2}$
所以二面角M-PQ-B為60°…(12分)
點評 本題考查滿足條件的平面的作法,考查二面角的大小的求法,考查空間中線線、線面、面面間的位置關系,考查推理論證能力、運算求解能力,考查化歸與轉化思想、數形結合思想,是中檔題.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 若x>0,則x>sinx恒成立 | |
| B. | 命題“若x-sinx=0,則x=0”的否命題為“若x-sinx≠0,則x≠0” | |
| C. | “命題p∧q為真”是“命題p∨q為真”的充分不必要條件 | |
| D. | 命題“?x∈R,x-lnx>0”的否定是“?x0∈R,x0-lnx0<0” |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | cosα-sinα | B. | sinα+cosα+2 | C. | sinα-cosα | D. | -sinα-cosα-2 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com