
【題目】已知函數![]() 在點
在點![]() 處的切線方程為
處的切線方程為![]() .
.
(1)求![]() 、
、![]() ;
;
(2)設曲線![]() 與
與![]() 軸負半軸的交點為點
軸負半軸的交點為點![]() ,曲線在點
,曲線在點![]() 處的切線方程為
處的切線方程為![]() ,求證:對于任意的實數
,求證:對于任意的實數![]() ,都有
,都有![]() ;
;
(3)若關于![]() 的方程
的方程![]() 有兩個實數根
有兩個實數根![]() ,
,![]() ,且
,且![]() ,證明:
,證明:![]() .
.
【答案】(1)![]() ;(2)證明見解析;(3)證明見解析.
;(2)證明見解析;(3)證明見解析.
【解析】
(1)將點![]() 代入切線方程得出
代入切線方程得出![]() ,并求出函數
,并求出函數![]() 的導數
的導數![]() ,由
,由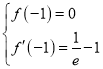 求出
求出![]() 、
、![]() 的值;
的值;
(2)求出點![]() 的坐標,并利用導數求出函數
的坐標,并利用導數求出函數![]() 在點
在點![]() 處切線對應的函數
處切線對應的函數![]() ,然后構造函數
,然后構造函數![]() ,利用導數證明出
,利用導數證明出![]() ;
;
(3)求出方程![]() 的根
的根![]() ,利用函數
,利用函數![]() 的單調性證明出
的單調性證明出![]() ,設函數
,設函數![]() 在原點處的切線對應的函數為
在原點處的切線對應的函數為![]() ,易得
,易得![]() 的根為
的根為![]() ,由函數
,由函數![]() 的單調性得出
的單調性得出![]() ,再利用不等式的性質可證明結論成立.
,再利用不等式的性質可證明結論成立.
(1)將![]() 代入切線方程
代入切線方程![]() 中,有
中,有![]() ,
,
所以![]() ,即
,即![]() ,
,
又![]() ,所以
,所以![]() ,
,
若![]() ,則
,則![]() ,與
,與![]() 矛盾,故
矛盾,故![]() ;
;
(2)由(1)可知![]() ,令
,令![]() ,有
,有![]() 或
或![]() ,
,
故曲線![]() 與
與![]() 軸負半軸的唯一交點
軸負半軸的唯一交點![]() 為
為![]() .
.
曲線在點![]() 處的切線方程為
處的切線方程為![]() ,則
,則![]() ,
,
令![]() ,則
,則![]() ,
,
所以![]() ,
,![]() .
.
當![]() 時,若
時,若![]() ,
,![]() ,
,
若![]() ,
,![]() ,
,![]() 在
在![]() 上單調遞增,
上單調遞增,![]() ,故
,故![]() ,
,![]() 在
在![]() 上單調遞減,
上單調遞減,
當![]() 時,由
時,由![]() 知
知![]() 在
在![]() 時單調遞增,
時單調遞增,![]() ,函數
,函數![]() 在
在![]() 上單調遞增.
上單調遞增.
所以![]() ,即
,即![]() 成立;
成立;
(3)![]() ,設
,設![]() 的根為
的根為![]() ,則
,則![]() ,
,
又![]() 單調遞減,且
單調遞減,且![]() ,所以
,所以![]() ,
,
設曲線![]() 在點
在點![]() 處的切線方程為
處的切線方程為![]() ,有
,有![]() ,
,
令![]() ,
,![]() ,
,
當![]() 時,
時,![]() ,
,
當![]() 時,
時,![]() ,
,
故函數![]() 在
在![]() 上單調遞增,又
上單調遞增,又![]() ,
,
所以當![]() 時,
時,![]() ,當
,當![]() 時,
時,![]() ,
,
所以函數![]() 在區間
在區間![]() 上單調遞減,在區間
上單調遞減,在區間![]() 上單調遞增,
上單調遞增,
所以![]() ,即
,即![]() ,
,
設![]() 的根為
的根為![]() ,則
,則![]() ,
,
又函數![]() 單調遞增,故
單調遞增,故![]() ,故
,故![]() .
.
又![]() ,所以
,所以![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的一個焦點與拋物線
的一個焦點與拋物線![]() 的焦點重合,且此拋物線的準線被橢圓
的焦點重合,且此拋物線的準線被橢圓![]() 截得的弦長為
截得的弦長為![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)直線![]() 交橢圓
交橢圓![]() 于
于![]() 、
、![]() 兩點,線段
兩點,線段![]() 的中點為
的中點為![]() ,直線
,直線![]() 是線段
是線段![]() 的垂直平分線,試問直線
的垂直平分線,試問直線![]() 是否過定點?若是,請求出該定點的坐標;若不是,請說明理由.
是否過定點?若是,請求出該定點的坐標;若不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠利用隨機數表對生產的600個零件進行抽樣測試,先將600個零件進行編號,編號分別為001,002,![]() ,599,600從中抽取60個樣本,如下提供隨機數表的第4行到第6行:
,599,600從中抽取60個樣本,如下提供隨機數表的第4行到第6行:
32 21 18 34 29 78 64 54 07 32 52 42 06 44 38 12 23 43 56 77 35 78 90 56 42
84 42 12 53 31 34 57 86 07 36 25 30 07 32 86 23 45 78 89 07 23 68 96 08 04
32 56 78 08 43 67 89 53 55 77 34 89 94 83 75 22 53 55 78 32 45 77 89 23 45
若從表中第6行第6列開始向右依次讀取3個數據,則得到的第6個樣本編號![]()
![]()
A. 522B. 324C. 535D. 578
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一商場對每天進店人數和商品銷售件數進行了統計對比,得到如下表格:
人數 | 10 | 15 | 20 | 25 | 30 | 35 | 40 |
件數 | 4 | 7 | 12 | 15 | 20 | 23 | 27 |
(1)在答題卡給定的坐標系中畫出表中數據的散點圖,并由散點圖判斷銷售件數![]() 與進店人數
與進店人數![]() 是否線性相關?(給出判斷即可,不必說明理由);
是否線性相關?(給出判斷即可,不必說明理由);
(2)建立![]() 關于
關于![]() 的回歸方程(系數精確到0.01),預測進店人數為80時,商品銷售的件數(結果保留整數).
的回歸方程(系數精確到0.01),預測進店人數為80時,商品銷售的件數(結果保留整數).
(參考數據:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
參考公式: ,
,![]() ,其中
,其中![]() ,
,![]() 為數據
為數據![]() 的平均數.
的平均數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】大學先修課程,是在高中開設的具有大學水平的課程,旨在讓學有余力的高中生早接受大學思維方式、學習方法的訓練,為大學學習乃至未來的職業生涯做好準備.某高中成功開設大學先修課程已有兩年,共有250人參與學習先修課程.
(Ⅰ)這兩年學校共培養出優等生150人,根據下圖等高條形圖,填寫相應列聯表,并根據列聯表檢驗能否在犯錯的概率不超過0.01的前提下認為學習先修課程與優等生有關系?

優等生 | 非優等生 | 總計 | |
學習大學先修課程 | 250 | ||
沒有學習大學先修課程 | |||
總計 | 150 |
(Ⅱ)某班有5名優等生,其中有2名參加了大學生先修課程的學習,在這5名優等生中任選3人進行測試,求這3人中至少有1名參加了大學先修課程學習的概率.
參考數據:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
參考公式:![]() ,其中
,其中![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖放置的邊長為1的正方形![]() 沿
沿![]() 軸滾動,點
軸滾動,點![]() 恰好經過原點.設頂點
恰好經過原點.設頂點![]() 的軌跡方程是
的軌跡方程是![]() ,則對函數
,則對函數![]() 有下列判斷:①函數
有下列判斷:①函數![]() 是偶函數;②對任意的
是偶函數;②對任意的![]() ,都有
,都有![]() ;③函數
;③函數![]() 在區間
在區間![]() 上單調遞減;④函數
上單調遞減;④函數![]() 的值域是
的值域是![]() ;⑤
;⑤![]() .其中判斷正確的序號是__________.
.其中判斷正確的序號是__________.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從某企業生產的某種產品中抽取100件,測量這些產品的一項質量指標值,由測量表得如下頻數分布表:
質量指標值分組 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125) |
頻數 | 6 | 26 | 38 | 22 | 8 |
(I)在答題卡上作出這些數據的頻率分布直方圖:
(II)估計這種產品質量指標值的平均數及方差(同一組中的數據用該組區間的中點值作代表);
(III)根據以上抽樣調查數據,能否認為該企業生產的這種產品符合“質量指標值不低于95的產品至少要占全部產品的80%”的規定?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知棱長為1的正方體![]() ,點
,點![]() 是四邊形
是四邊形![]() 內(含邊界)任意一點,
內(含邊界)任意一點,![]() 是
是![]() 中點,有下列四個結論:
中點,有下列四個結論:
①![]() ;②當
;②當![]() 點為
點為![]() 中點時,二面角
中點時,二面角![]() 的余弦值
的余弦值![]() ;③
;③![]() 與
與![]() 所成角的正切值為
所成角的正切值為![]() ;④當
;④當![]() 時,點
時,點![]() 的軌跡長為
的軌跡長為![]() .
.
其中所有正確的結論序號是( )
A.①②③B.①③④C.②③④D.①②④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某調研機構,對本地![]() 歲的人群隨機抽取
歲的人群隨機抽取![]() 人進行了一次生活習慣是否符合低碳觀念的調查,將生活習慣符合低碳觀念的稱為“低碳族”,否則稱為“非低碳族”,結果顯示,有
人進行了一次生活習慣是否符合低碳觀念的調查,將生活習慣符合低碳觀念的稱為“低碳族”,否則稱為“非低碳族”,結果顯示,有![]() 人為“低碳族”,該
人為“低碳族”,該![]() 人的年齡情況對應的頻率分布直方圖如圖.
人的年齡情況對應的頻率分布直方圖如圖.

(1)根據頻率分布直方圖,估計這![]() 名“低碳族”年齡的平均值,中位數;
名“低碳族”年齡的平均值,中位數;
(2)若在“低碳族”且年齡在![]() 、
、![]() 的兩組人群中,用分層抽樣的方法抽取
的兩組人群中,用分層抽樣的方法抽取![]() 人,試估算每個年齡段應各抽取多少人?
人,試估算每個年齡段應各抽取多少人?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com