
【題目】已知橢圓![]() 的一個焦點與拋物線
的一個焦點與拋物線![]() 的焦點重合,且此拋物線的準線被橢圓
的焦點重合,且此拋物線的準線被橢圓![]() 截得的弦長為
截得的弦長為![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)直線![]() 交橢圓
交橢圓![]() 于
于![]() 、
、![]() 兩點,線段
兩點,線段![]() 的中點為
的中點為![]() ,直線
,直線![]() 是線段
是線段![]() 的垂直平分線,試問直線
的垂直平分線,試問直線![]() 是否過定點?若是,請求出該定點的坐標;若不是,請說明理由.
是否過定點?若是,請求出該定點的坐標;若不是,請說明理由.
【答案】(1)![]() ;(2)直線
;(2)直線![]() 過定點
過定點![]() ,詳見解析.
,詳見解析.
【解析】
(1)由題意得出![]() ,由題意知點
,由題意知點![]() 在橢圓
在橢圓![]() 上,由此得出關于
上,由此得出關于![]() 、
、![]() 的方程組,求出
的方程組,求出![]() 、
、![]() 的值,即可得出橢圓
的值,即可得出橢圓![]() 的標準方程;
的標準方程;
(2)解法一:由題意可知,直線![]() 的斜率不為零,然后分直線
的斜率不為零,然后分直線![]() 的斜率存在且不為零和直線
的斜率存在且不為零和直線![]() 的斜率不存在兩種情況討論,在第一種情況下,設直線
的斜率不存在兩種情況討論,在第一種情況下,設直線![]() 的方程為
的方程為![]() ,設點
,設點![]() 、
、![]() ,將直線
,將直線![]() 的方程與橢圓
的方程與橢圓![]() 的方程聯立,列出韋達定理,由
的方程聯立,列出韋達定理,由![]() 得出
得出![]() ,并寫出直線
,并寫出直線![]() 的方程,由此可得出直線
的方程,由此可得出直線![]() 所過定點的坐標;在第二種情況下可得出直線
所過定點的坐標;在第二種情況下可得出直線![]() 為
為![]() 軸,即可得出直線
軸,即可得出直線![]() 過定點
過定點![]() ,由此得出結論;
,由此得出結論;
解法二:由題意可知,直線![]() 的斜率不為零,然后分直線
的斜率不為零,然后分直線![]() 的斜率存在且不為零和直線
的斜率存在且不為零和直線![]() 的斜率不存在兩種情況討論,在第一種情況下,由點差法可得出直線
的斜率不存在兩種情況討論,在第一種情況下,由點差法可得出直線![]() 的斜率為
的斜率為![]() ,可寫出直線
,可寫出直線![]() 的方程,即可得出直線
的方程,即可得出直線![]() 所過定點的坐標;在第二種情況下可得出直線
所過定點的坐標;在第二種情況下可得出直線![]() 為
為![]() 軸,即可得出直線
軸,即可得出直線![]() 過定點
過定點![]() ,由此得出結論.
,由此得出結論.
(1)拋物線![]() 的焦點為
的焦點為![]() ,準線為
,準線為![]() .
.
由于拋物線![]() 的準線
的準線![]() 截橢圓
截橢圓![]() 所得弦長為
所得弦長為![]() ,
,
則點![]() 在橢圓
在橢圓![]() 上,則有
上,則有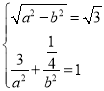 ,解得
,解得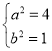 ,
,
因此,橢圓![]() 的標準方程為
的標準方程為![]() ;
;
(2)法一:顯然點![]() 在橢圓
在橢圓![]() 內部,故
內部,故![]() ,且直線
,且直線![]() 的斜率不為
的斜率不為![]() .
.
當直線![]() 的斜率存在且不為
的斜率存在且不為![]() 時,易知
時,易知![]() ,設直線
,設直線![]() 的方程為
的方程為![]() ,
,
代入橢圓方程并化簡得:![]() .
.
設![]() ,
,![]() ,則
,則![]() ,解得
,解得![]() .
.
因為直線![]() 是線段
是線段![]() 的垂直平分線,
的垂直平分線,
故直線![]() 的方程為
的方程為![]() ,即
,即![]() ,即
,即![]() .
.
令![]() ,此時
,此時![]() ,
,![]() ,于是直線
,于是直線![]() 過定點
過定點![]() ;
;
當直線![]() 的斜率不存在時,易知
的斜率不存在時,易知![]() ,此時直線
,此時直線![]() ,故直線
,故直線![]() 過定點
過定點![]() .
.
綜上所述,直線![]() 過定點
過定點![]() ;
;
法二:顯然點![]() 在橢圓
在橢圓![]() 內部,故
內部,故![]() ,且直線
,且直線![]() 的斜率不為
的斜率不為![]() .
.
當直線![]() 的斜率存在且不為
的斜率存在且不為![]() 時,設
時,設![]() ,
,![]() ,
,
則有![]() ,
,![]() ,
,
兩式相減得![]() ,
,
由線段![]() 的中點為
的中點為![]() ,則
,則![]() ,
,![]() ,
,
故直線![]() 的斜率
的斜率![]() ,
,
因為直線![]() 是線段
是線段![]() 的垂直平分線,
的垂直平分線,
故直線![]() 的方程為
的方程為![]() ,即
,即![]() ,即
,即![]() .
.
令![]() ,此時
,此時![]() ,
,![]() ,于是直線
,于是直線![]() 過定點
過定點![]() ;
;
當直線![]() 的斜率不存在時,易知
的斜率不存在時,易知![]() ,此時直線
,此時直線![]() ,故直線
,故直線![]() 過定點
過定點![]()
綜上所述,直線![]() 過定點
過定點![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】為了紀念“一帶一路”倡議提出五周年,某城市舉辦了一場知識競賽,為了了解市民對“一帶一路”知識的掌握情況,從回收的有效答卷中按青年組和老年組各隨機抽取了40份答卷,發現成績都在![]() 內,現將成績按區間
內,現將成績按區間![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 進行分組,繪制成如下的頻率分布直方圖.
進行分組,繪制成如下的頻率分布直方圖.
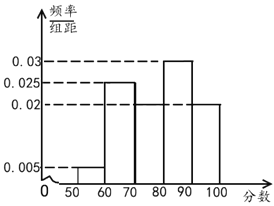
青年組

中老年組
(1)利用直方圖估計青年組的中位數和老年組的平均數;
(2)從青年組![]() ,
,![]() 的分數段中,按分層抽樣的方法隨機抽取5份答卷,再從中選出3份答卷對應的市民參加政府組織的座談會,求選出的3位市民中有2位來自
的分數段中,按分層抽樣的方法隨機抽取5份答卷,再從中選出3份答卷對應的市民參加政府組織的座談會,求選出的3位市民中有2位來自![]() 分數段的概率.
分數段的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖1,已知菱形![]() 的對角線
的對角線![]() 交于點
交于點![]() ,點
,點![]() 為線段
為線段![]() 的中點,
的中點,![]() ,
,![]() ,將三角形
,將三角形![]() 沿線段
沿線段![]() 折起到
折起到![]() 的位置,
的位置,![]() ,如圖2所示.
,如圖2所示.

(Ⅰ)證明:平面![]()
![]() 平面
平面![]() ;
;
(Ⅱ)求三棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現將甲、乙兩個學生在高二的6次數學測試的成績(百分制)制成如圖所示的莖葉圖,進入高三后,由于改進了學習方法,甲、乙這兩個學生的考試成績預計同時有了大的提升:若甲(乙)的高二任意一次考試成績為![]() ,則甲(乙)的高三對應的考試成績預計為
,則甲(乙)的高三對應的考試成績預計為![]() .
.

(1)試預測:高三6次測試后,甲、乙兩個學生的平均成績分別為多少?誰的成績更穩定?
(2)若已知甲、乙兩個學生的高二6次考試成績分別由低到高進步的,定義![]() 為高三的任意一次考試后甲、乙兩個學生的當次成績之差的絕對值,求
為高三的任意一次考試后甲、乙兩個學生的當次成績之差的絕對值,求![]() 的平均值.
的平均值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】身體素質拓展訓練中,人從豎直墻壁的頂點A沿光滑桿自由下滑到傾斜的木板上(人可看作質點),若木板的傾斜角不同,人沿著三條不同路徑AB、AC、AD滑到木板上的時間分別為t1、t2、t3,若已知AB、AC、AD與板的夾角分別為70o、90o和105o,則( )

A. t1>t2>t3 B. t1<t2<t3 C. t1=t2=t3 D. 不能確定t1、t2、t3之間的關系
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年“非洲豬瘟”過后,全國生豬價格逐步上漲,某大型養豬企業,欲將達到養殖周期的生豬全部出售,根據去年的銷售記錄,得到銷售生豬的重量的頻率分布直方圖(如圖所示).
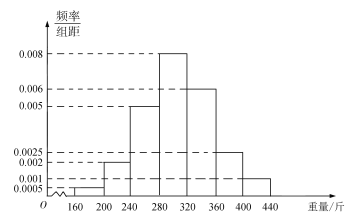
(1)根據去年生豬重量的頻率分布直方圖,估計今年生豬出欄(達到養殖周期)時,生豬重量達不到270斤的概率(以頻率代替概率);
(2)若假設該企業今年達到養殖周期的生豬出欄量為5000頭,生豬市場價格是8元/斤,試估計該企業本養殖周期的銷售收入是多少萬元;
(3)若從本養殖周期的生豬中,任意選兩頭生豬,其重量達到270斤及以上的生豬數為隨機變量![]() ,試求隨機變量
,試求隨機變量![]() 的分布列及方差.
的分布列及方差.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱錐![]() 中,N為CD的中點,M是AC上一點.
中,N為CD的中點,M是AC上一點.
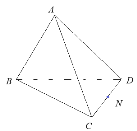
(1)若M為AC的中點,求證:AD//平面BMN;
(2)若![]() ,平面
,平面![]() 平面BCD,
平面BCD,![]() ,求直線AC與平面BMN所成的角的余弦值。
,求直線AC與平面BMN所成的角的余弦值。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 在點
在點![]() 處的切線方程為
處的切線方程為![]() .
.
(1)求![]() 、
、![]() ;
;
(2)設曲線![]() 與
與![]() 軸負半軸的交點為點
軸負半軸的交點為點![]() ,曲線在點
,曲線在點![]() 處的切線方程為
處的切線方程為![]() ,求證:對于任意的實數
,求證:對于任意的實數![]() ,都有
,都有![]() ;
;
(3)若關于![]() 的方程
的方程![]() 有兩個實數根
有兩個實數根![]() ,
,![]() ,且
,且![]() ,證明:
,證明:![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com