
 如圖,三角形PDC所在的平面與長方形ABCD所在的平面垂直,
如圖,三角形PDC所在的平面與長方形ABCD所在的平面垂直,分析 (1)利用平面與平面垂直的性質定理得出BC⊥平面PDC,即可證明BC⊥PD;
(2)利用等體積法,求點C到平面PDA的距離.
解答 (1)證明:因為四邊形ABCD是長方形,所以BC⊥CD,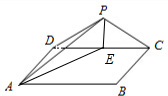
因為平面PDC⊥平面ABCD,平面PDC∩平面ABCD=CD,BC?面ABCD,
所以BC⊥平面PDC,
因為PD?平面PDC,
所以BC⊥PD;
(2)解:取CD的中點E,連接AE和PE,
因為PD=PC,所以PE⊥CD,
在Rt△PED中,PE=$\sqrt{16-9}$=$\sqrt{7}$.
因為平面PDC⊥平面ABCD,平面PDC∩平面ABCD=CD,PE?平面PDC,
所以PE⊥平面ABCD.
由(1)知:BC⊥平面PDC,
因為四邊形ABCD是長方形,所以BC∥AD,
所以AD⊥平面PDC,
因為PD?平面PDC,所以AD⊥PD.
設點C到平面PDA的距離為h.
因為VC-PDA=VP-ACD,
所以h=$\frac{\frac{1}{2}×3×6×\sqrt{7}}{\frac{1}{2}×3×4}$=$\frac{3\sqrt{7}}{2}$,所以點C到平面PDA的距離是$\frac{3\sqrt{7}}{2}$.
點評 本題考查平面與平面垂直的性質,線面垂直與線線垂直的判定,考查三棱錐體積等知識,注意解題方法的積累,屬于中檔題.


科目:高中數學 來源: 題型:選擇題
| A. | $\frac{{\sqrt{10}}}{10}$ | B. | $\frac{{\sqrt{10}}}{10}$ | C. | $\frac{{\sqrt{10}}}{5}$ | D. | $\frac{{\sqrt{15}}}{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| 分數 | [50,59) | [60,69) | [70,79) | [80,89) | [90,100) |
| 甲班頻數 | 5 | 6 | 4 | 4 | 1 |
| 乙班頻數 | 1 | 3 | 6 | 5 |
| 甲班 | 乙班 | 總計 | |
| 成績優良 | |||
| 成績不優良 | |||
| 總計 |
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
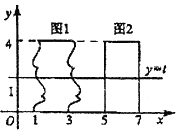 我國南北朝時代的數學家祖暅提出體積的計算原理(組暅原理):“冪勢既同,則積不容異”.“勢”即是高,“冪”是面積.意思是:如果兩等高的幾何體在同高處裁得兩幾何體的裁面積恒等,那么這兩個幾何體的體積相等,類比祖暅原理,如圖所示,在平面直角坐標系中,圖1是一個形狀不規則的封閉圖形,圖2是一個矩形,且當實數t取[0,4]上的任意值時,直線y=t被圖1和圖2所截得的線段始終相等,則圖1的面積為8.
我國南北朝時代的數學家祖暅提出體積的計算原理(組暅原理):“冪勢既同,則積不容異”.“勢”即是高,“冪”是面積.意思是:如果兩等高的幾何體在同高處裁得兩幾何體的裁面積恒等,那么這兩個幾何體的體積相等,類比祖暅原理,如圖所示,在平面直角坐標系中,圖1是一個形狀不規則的封閉圖形,圖2是一個矩形,且當實數t取[0,4]上的任意值時,直線y=t被圖1和圖2所截得的線段始終相等,則圖1的面積為8.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 2 | B. | 4 | C. | $\sqrt{5}$-1 | D. | $\sqrt{5}$+1 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| 學生 | A1 | A2 | A3 | A4 | A5 |
| 數學x(分) | 89 | 91 | 93 | 95 | 97 |
| 物理y(分) | 87 | 89 | 89 | 92 | 93 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -$\frac{16}{65}$ | B. | $\frac{16}{65}$ | C. | -$\frac{56}{65}$ | D. | $\frac{56}{65}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com