
如圖,在四棱錐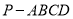 中,底面
中,底面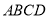 是邊長為
是邊長為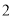 的正方形,側面
的正方形,側面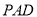
底面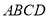 ,且
,且 ,
,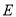 、
、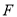 分別為
分別為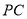 、
、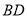 的中點.
的中點.
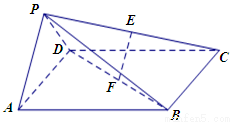
(1)求證: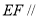 平面
平面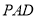 ;
;
(2)求證:面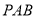
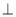 平面
平面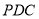 ;
;
(3)在線段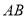 上是否存在點
上是否存在點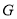 ,使得二面角
,使得二面角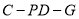 的余弦值為
的余弦值為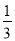 ?說明理由.
?說明理由.
(1)詳見解析;(2)詳見解析;(3)線段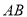 上存在點
上存在點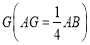 ,使得二面角
,使得二面角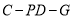 的余弦值為
的余弦值為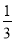 .
.
【解析】
試題分析:(1)連接 經過點
經過點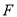 ,利用中位線得到
,利用中位線得到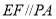 ,再由直線與平面平行的判定定理得到
,再由直線與平面平行的判定定理得到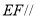
平面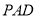 ;(2)利用平面與平面垂直的性質定理結合側面
;(2)利用平面與平面垂直的性質定理結合側面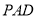
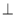 底面
底面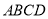 得到
得到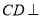 平面
平面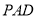 ,從而得到
,從而得到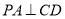 ,再由勾股定理證明
,再由勾股定理證明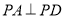 ,結合直線與平面垂直的判定定理證明
,結合直線與平面垂直的判定定理證明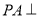 平面
平面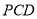 ,最后利用平面與平面垂直的判定定理得到平面
,最后利用平面與平面垂直的判定定理得到平面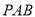
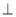 平面
平面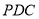 ;(3)取
;(3)取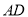 的中點
的中點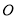 ,連接
,連接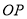 、
、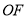 ,
,
利用平面與平面垂直的性質定理證明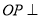 平面
平面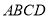 ,然后以點
,然后以點 為坐標原點,
為坐標原點,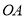 、
、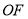 、
、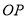 所在直線分別為
所在直線分別為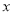 軸、
軸、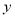 軸、
軸、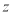 軸建立空間直角坐標系
軸建立空間直角坐標系 ,利用空間向量法解決題中二面角問題.
,利用空間向量法解決題中二面角問題.
(1)證明:連接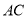 ,由正方形性質可知,
,由正方形性質可知,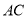 與
與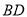 相交于
相交于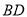 的中點
的中點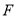 ,
,
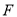 也為
也為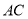 中點,
中點,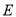 為
為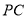 中點.
中點.
所以在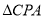 中,
中,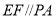 ,
,
又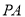
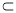 平面
平面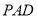 ,
,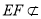 平面
平面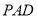 ,
,
所以 平面
平面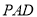 ;
;
(2)證明:因為平面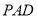
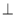 平面
平面 ,平面
,平面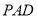
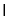 面
面
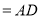
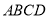 為正方形,
為正方形,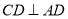 ,
,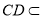 平面
平面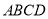 ,所以
,所以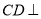 平面
平面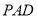 .
.
又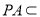 平面
平面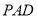 ,所以
,所以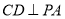 .
.
又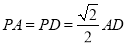 ,所以
,所以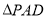 是等腰直角三角形,且
是等腰直角三角形,且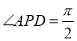 ,即
,即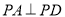 .
.
又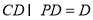 ,且
,且 、
、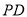
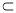 面
面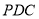 ,所以
,所以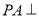 面
面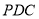 .
.
又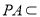 面
面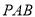 ,所以面
,所以面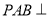 面
面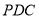 ;
;
(3)取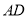 的中點
的中點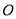 ,連接
,連接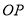 、
、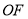 ,因為
,因為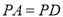 ,所以
,所以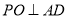 .
.
又側面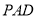
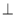 底面
底面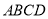 ,平面
,平面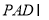 平面
平面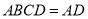 ,所以
,所以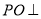 平面
平面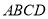 .
.
而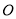 、
、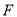 分別為
分別為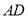 、
、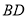 的中點,所以
的中點,所以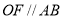 ,
,
又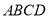 是正方形,故
是正方形,故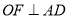 .
.
以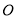 為原點,建立空間直角坐標系
為原點,建立空間直角坐標系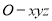 ,
,
則有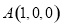 ,
,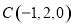 ,
,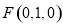 ,
,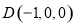 ,
,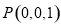 ,
,
若在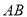 上存在點
上存在點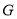 ,使得二面角
,使得二面角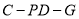 的余弦值為
的余弦值為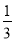 ,連接
,連接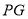 、
、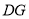 ,
,
設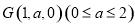 ,
,
則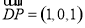 ,
,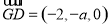 ,由(2)知平面
,由(2)知平面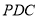 的法向量為
的法向量為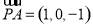 ,
,
設平面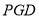 的法向量為
的法向量為 .則
.則 ,即
,即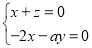 ,解得
,解得 ,
,
令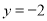 ,得
,得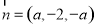 ,
,
所以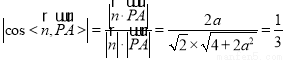 ,解得
,解得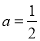 (舍去
(舍去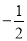 ).
).
所以,線段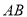 上存在點
上存在點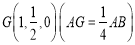 ,使得二面角
,使得二面角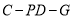 的余弦值為
的余弦值為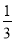 .
.
考點:1.直線與平面平行;2.平面與平面垂直的性質與判定;3.利用空間向量法處理二面角


 開心試卷期末沖刺100分系列答案
開心試卷期末沖刺100分系列答案 雙基同步導航訓練系列答案
雙基同步導航訓練系列答案科目:高中數學 來源:2013-2014學年廣東省揭陽市高三3月第一次模擬考試文科數學試卷(解析版) 題型:選擇題
下列函數是偶函數,且在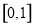 上單調遞增的是( )
上單調遞增的是( )
A.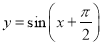 B.
B.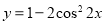 C.
C.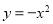 D.
D.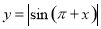
查看答案和解析>>
科目:高中數學 來源:2013-2014學年廣東省廣州市畢業班綜合測試二理科數學試卷(解析版) 題型:選擇題
有兩張卡片,一張的正反面分別寫著數字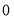 與
與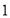 ,另一張的正反面分別寫著數字
,另一張的正反面分別寫著數字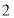 與
與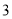 ,將兩張卡片排在一起組成一個兩位數,則所組成的兩位數為奇數的概率是( )
,將兩張卡片排在一起組成一個兩位數,則所組成的兩位數為奇數的概率是( )
A.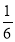 B.
B.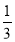 C.
C.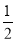 D.
D.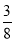
查看答案和解析>>
科目:高中數學 來源:2013-2014學年廣東省廣州市畢業班綜合測試二文科數學試卷(解析版) 題型:選擇題
設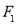 、
、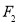 分別是橢圓
分別是橢圓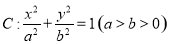 的左、右焦點,點
的左、右焦點,點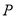 在橢圓
在橢圓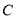 上,線段
上,線段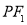 的中點在
的中點在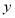 軸上,若
軸上,若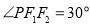 ,則橢圓的離心率為( )
,則橢圓的離心率為( )
A.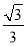 B.
B.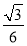 C.
C.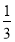 D.
D.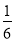
查看答案和解析>>
科目:高中數學 來源:2013-2014學年廣東省東莞市高三第二次模擬考試理科數學試卷(解析版) 題型:填空題
已知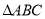 的內角
的內角 、
、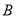 、
、 的對邊分別為
的對邊分別為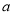 、
、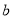 、
、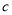 ,且
,且 ,
,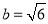 ,
,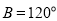 ,則
,則
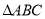 的面積等于________.
的面積等于________.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年廣東省東莞市高三第二次模擬考試理科數學試卷(解析版) 題型:選擇題
已知平面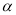 、
、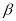 和直線
和直線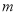 ,給出條件:①
,給出條件:①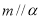 ;②
;②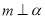 ;③
;③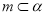 ;④
;④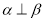 ;⑤
;⑤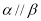 .
.
由這五個條件中的兩個同時成立能推導出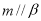 的是( )
的是( )
A.①④ B.①⑤ C.②⑤ D.③⑤
查看答案和解析>>
科目:高中數學 來源:2013-2014學年廣東省東莞市高三第二次模擬考試文科數學試卷(解析版) 題型:選擇題
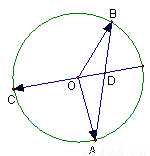
如圖所示,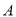 、
、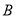 、
、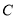 是圓
是圓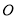 上的三點,
上的三點,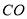 的延長線與線段
的延長線與線段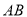 交于圓內一點
交于圓內一點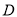 ,若
,若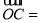
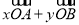 ,則 ( )
,則 ( )
A.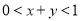 B.
B.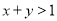
C.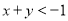 D.
D.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com