
分析 (1)由正弦定理,三角形內角和定理,兩角和的正弦函數公式,化簡已知可得2sinAcosC=-sinA,結合sinA≠0,可求cosC=-$\frac{1}{2}$,結合范圍0<C<π,可求C的值.
(2)由(1)及三角函數恒等變換化簡可得sinAsinB=$\frac{1}{2}$sin(2A+$\frac{π}{6}$)-$\frac{1}{4}$,結合范圍0<A<$\frac{π}{3}$,利用正弦函數的圖象和性質可求最大值.
解答 (本題滿分為12分)
解:(1)因為:$\frac{2a+b}{cosB}$=$\frac{-c}{cosC}$,
所以:由正弦定理可得:$\frac{2sinA+sinB}{cosB}$=$\frac{-sinC}{cosC}$,
所以:2sinAcosC=-(sinBcosC+sinCcosB)=-sinA.
因為:sinA≠0,
所以:cosC=-$\frac{1}{2}$.
又因為:0<C<π,
故C=$\frac{2π}{3}$. …(5分)
(2)因為:sinAsinB=sinAsin($\frac{π}{3}$-A)=sinA($\frac{\sqrt{3}}{2}$cosA-$\frac{1}{2}$sinA)
=$\frac{\sqrt{3}}{4}$sin2A-$\frac{1}{2}$sin2A=$\frac{\sqrt{3}}{4}$sin2A-$\frac{1-cos2A}{4}$
=$\frac{1}{2}$sin(2A+$\frac{π}{6}$)-$\frac{1}{4}$.
因為:0<A<$\frac{π}{3}$,
所以:當A=$\frac{π}{6}$時,sinAsinB有最大值為$\frac{1}{4}$.…(12分)
點評 本題主要考查了正弦定理,三角形內角和定理,兩角和的正弦函數公式,三角函數恒等變換,正弦函數的圖象和性質在解三角形中的綜合應用,考查了計算能力和轉化思想,屬于中檔題.


科目:高中數學 來源: 題型:選擇題
| A. | 8$\sqrt{5}$ | B. | 4$\sqrt{5}$ | C. | 12 | D. | 24 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
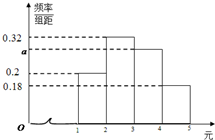 甲、乙、丙三人參加微信群搶紅包游戲,規則如下:每輪游戲發50個紅包,每個紅包金額為x元,x∈[1,5].已知在每輪游戲中所產生的50個紅包金額的頻率分布直方圖如圖所示.
甲、乙、丙三人參加微信群搶紅包游戲,規則如下:每輪游戲發50個紅包,每個紅包金額為x元,x∈[1,5].已知在每輪游戲中所產生的50個紅包金額的頻率分布直方圖如圖所示.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 如圖,已知四棱錐P-ABCD中,底面ABCD是直角梯形,∠ADC=90°,AB∥CD,AD=DC=$\frac{1}{2}$AB=$\sqrt{2}$,平面PBC⊥平面ABCD.
如圖,已知四棱錐P-ABCD中,底面ABCD是直角梯形,∠ADC=90°,AB∥CD,AD=DC=$\frac{1}{2}$AB=$\sqrt{2}$,平面PBC⊥平面ABCD.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源:2017屆安徽合肥一中高三上學期月考一數學(理)試卷(解析版) 題型:選擇題
設命題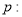 函數
函數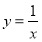 在定義域上為減函數,命題
在定義域上為減函數,命題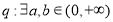 ,當
,當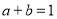 時,
時,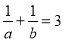 ,以下說法正確的是( )
,以下說法正確的是( )
A.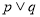 為真 B.
為真 B.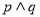 為真
為真
C.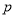 真
真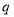 假 D.
假 D. 均假
均假
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com