考點：直線與圓的位置關(guān)系
專題：直線與圓
分析：設(shè)3x-4y=b，利用直線和圓的位置關(guān)系即可得到結(jié)論．
解答：
解：設(shè)3x-4y=b，即3x-4y-b=0，
則圓心到直線的距離d=
=≤1，
即|b|≤5，
解得-5≤b≤5，
故3x-4y的最大值5．
點評：本題主要考查直線和圓的位置關(guān)系的應(yīng)用，比較基礎(chǔ)．
練習(xí)冊系列答案
相關(guān)習(xí)題
科目：高中數(shù)學(xué)
來源：
題型：
方程3x
2+6x-
=0的實數(shù)根個數(shù)為
．
查看答案和解析>>
科目：高中數(shù)學(xué)
來源：
題型：
y=x|x|+3的單調(diào)增區(qū)間是
．
查看答案和解析>>
科目：高中數(shù)學(xué)
來源：
題型：
已知函數(shù)f（x）=log2（ax2+2x+3）
（1）若f（1）=1，求f（x）的單調(diào)區(qū)間；
（2）若已知函數(shù)的值域為R，求a的取值范圍；
（3）是否存在實數(shù)a，使f（x）的最小值為0？若存在，求出a的值；若不存在，說明理由．
查看答案和解析>>
科目：高中數(shù)學(xué)
來源：
題型：
如圖所示，在河岸 ac一側(cè)測量河的寬度，測量以下四組數(shù)據(jù)，較適宜的是（ ）
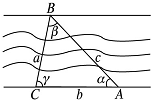
| A、c，α，γ |
| B、c，b，α |
| C、c，a，β |
| D、b，α，γ |
查看答案和解析>>
科目：高中數(shù)學(xué)
來源：
題型：
函數(shù)f（x）=log
2x-
+a的一個零點在（1，4）內(nèi)，則實數(shù)a的取值范圍為（ ）
| A、（-，2） |
| B、（4，6） |
| C、（2，4） |
| D、（-3，-） |
查看答案和解析>>
科目：高中數(shù)學(xué)
來源：
題型：
已知點M（0，1），C（2，3），動點P滿足|
|=1，過點M且斜率為k的直線l與動點P的軌跡相交于A、B兩點．
（1）求動點P的軌跡方程；
（2）求實數(shù)k的取值范圍；
（3）求證：
•
為定值；
（4）若O為坐標(biāo)原點，且
•
=12，求直線l的方程．
查看答案和解析>>
科目：高中數(shù)學(xué)
來源：
題型：
已知橢圓
Г的方程為
+
=1（a＞b＞0）點A，B分別為Г上的兩個動點，O為坐標(biāo)原點，且OA⊥OB；其中OA，OB稱為橢圓的一條半徑．
（1）求證：
+
=
+
；|OA|
2+|OB|
2的最小值為
；
（2）過點O作OH⊥AB于H，求證：|OH|=
；S
△OAB的最小值是
；
（3）將（1）（2）的結(jié)論推廣至雙曲線，結(jié)論是否依然成立，若成立，證明你的結(jié)論；若不成立，請說明理由．
查看答案和解析>>
科目：高中數(shù)學(xué)
來源：
題型：
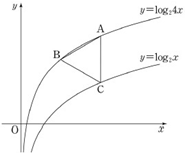
如圖所示，已知函數(shù)y=log
24x圖象上的兩點A，B和函數(shù)y=log
2x上的點 C，線段AC平行于y軸，三角形ABC為正三角形時，點B的坐標(biāo)為（p，q），則實數(shù)p的值為
．
查看答案和解析>>
科學(xué)實驗活動冊系列答案
