
分析 (Ⅰ)求出函數的導數,解關于導函數的不等式,求出函數的單調區間即可;(Ⅱ)通過討論a的范圍,求出函數f(x)在(0,a]的最大值即可.
解答 解:(Ⅰ)∵f(x)=lnx-x2+x+2,其定義域為(0,+∞),
∴f′(x)=$\frac{-(2x+1)(x-1)}{x}$,
∵x>0,∴當0<x<1時,f′(x)>0;當x>1時,f′(x)<0,
故函數f(x)的單調遞增區間是(0,1);單調遞減區間是(1,+∞).
(Ⅱ)由(Ⅰ)知,函數f(x)的單調遞增區間是(0,1);單調遞減區間是(1,+∞),
當0<a≤1時,f(x)在區間(0,a]上單調遞增,f(x)的最大值是f(a)=lna-a2+a+2;
當a>1時,f(x)在區間(0,1)上單調遞增,在(1,a)上單調遞減,
則f(x)在x=1處取得極大值,也即該函數在(0,a]上的最大值,此時f(x)的最大值是f(1)=2;
∴f(x)在區間(0,a]上的最大值f(a)=$\left\{\begin{array}{l}{lna{-a}^{2}+a+2,0<a≤1}\\{2,a>1}\end{array}\right.$.
點評 本題考查了函數的單調性、最值問題,考查導數的應用以及分類討論思想,是一道中檔題.


 智趣寒假作業云南科技出版社系列答案
智趣寒假作業云南科技出版社系列答案科目:高中數學 來源: 題型:選擇題
| A. | (-∞,1) | B. | (-∞,1] | C. | (-∞,-4)∪(-4,1] | D. | (-∞,-4)∪(-4,1) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
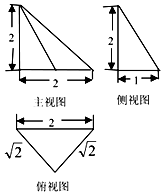
| A. | $\frac{1}{3}$ | B. | 1 | C. | $\frac{4}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
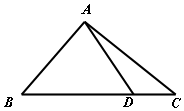 如圖,已知D是△ABC邊BC上一點.
如圖,已知D是△ABC邊BC上一點.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| 參加書法班 | 未參加書法班 | |
| 參加演講班 | 8 | 5 |
| 未參加演講班 | 2 | 33 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $2\sqrt{3}$ | B. | 9 | C. | $\frac{{9\sqrt{3}}}{2}$ | D. | $\frac{{9\sqrt{3}}}{4}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
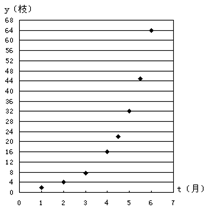 如圖給出了紅豆生長時間t(月)與枝數y(枝)的散點圖:那么“紅豆生南國,春來發幾枝.”的紅豆生長時間與枝數的關系用下列哪個函數模型擬合最好?( )
如圖給出了紅豆生長時間t(月)與枝數y(枝)的散點圖:那么“紅豆生南國,春來發幾枝.”的紅豆生長時間與枝數的關系用下列哪個函數模型擬合最好?( )| A. | 二次函數:y=2t2 | B. | 冪函數:y=t3 | ||
| C. | 指數函數:y=2t | D. | 對數函數:y=log2t |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (0,+∞) | B. | [2,+∞) | C. | (0,2] | D. | [2,4] |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com